Niveau maths sup

Energie potentielle ressort

Posté par
Aroust 04-09-17 à 15:17

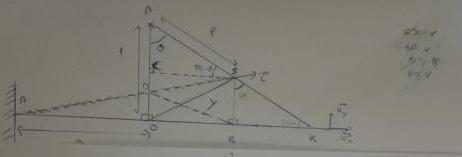
Bonjour, j'ai un exo où il faut calculer l?énergie potentielle d'un ressort. Pourtant, après 2 heures de recherche, je n'arrive pas à la même solution que mon prof. Je vous joins l'exos avec la réponse de mon prof entouré, et ce que j'ai fait. Donc voilà si vous pouviez me dire où je me trompe et comment arriver à la bonne réponse du coup, ce serait cool .

Energie potentielle ressort

***Un énoncé doit être recopié***

Posté par re : Energie potentielle ressort 04-09-17 à 15:18

voilà ce que j'ai fait

Energie potentielle ressort

***Image recadrée***

Posté par re : Energie potentielle ressort 04-09-17 à 15:40

Bonjour
Remarque préliminaire : tu as bien fait de scanner ton schéma. Pour le reste, il faut recopier l'énoncé et ce que tu as fait. Juste deux indications tout de même :

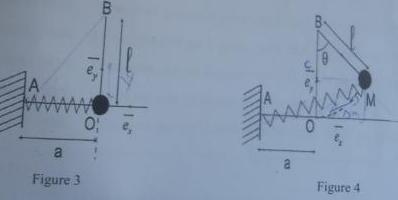
1° : le vecteur déplacement $\vec{OM}$ dans la base (e_x,e_y) a pour coordonnées :

$x=l.\sin\left(\theta\right)\quad;\quad y=l.\left[1-\cos\left(\theta\right)\right]$

L'énergie potentielle de pesanteur, en choisissant le niveau d'altitude nulle en y = 0 peut s'écrire :

$E_{pp}=m.g.y$

L'énergie potentielle élastique vaut :

$E_{pe}=\frac{1}{2}k\cdot\Vert\overrightarrow{OM}\Vert^{2}=\frac{1}{2}k\cdot\left(x^{2}+y^{2}\right)$

Posté par re : Energie potentielle ressort 04-09-17 à 15:58

Ah ok, bah justement c'est ça que je ne comprend pas : Pourquoi pour l'énergie potentielle élastique , l'élongation vaut OM ? A moins que j'ai mal compris mon cours, la valeur de l'élongation en valeur absolue vaut abs(l-l0) avec l0 la longueur à vide du ressort. Ce qui ici nous donnerait donc abs(AM-a) .

Posté par re : Energie potentielle ressort 04-09-17 à 19:12

Tu as raison dans le cas général. Contrairement à ce que suggère la figure fournie, il est nécessaire de supposer la longueur à vide du ressort très supérieure à la longueur du pendule pour obtenir l'expression fournie de l'énergie potentielle. Dans ces conditions, pour des valeurs de pas trop élevées (je suppose que par la suite, on étudie des oscillations de faible amplitude), l'axe du ressort reste constamment très proche du point O de sorte que (AM-a)²(OM)².
Ce qui est équivalent à supposer :
|y|<<|a+x|
et donc : (AM)-ax
et donc une énergie potentielle élastique très proche de
$\frac{1}{2}k\cdot x^{2}=\frac{1}{2}k\cdot l^{2}\cdot\sin^{2}\left(\theta\right)$ .
Cela peut d'ailleurs se retrouver en partant de l'expression rigoureuse de l'énergie potentielle élastique :

$E_{pe}=\frac{1}{2}k\left(\Vert\overrightarrow{AM}\Vert-a\right)^{2}=\frac{1}{2}k\left(\sqrt{\left(a+x\right)^{2}+y^{2}}-a\right)^{2}$

Si : $y^{2}\ll\left(a+x\right)^{2}$ , on obtient bien :
$E_{pe}\approx\frac{1}{2}k\cdot x^{2}$
J'ignore la suite du problème mais j'ai comme l'impression qu'il complique inutilement la situation...

Posté par re : Energie potentielle ressort 05-09-17 à 14:35

Dans mes messages précédents, je me suis focalisée sur l'expression "41" de l'énergie potentielle considérée comme vraie par ton professeur mais, comme je l'ai montrée, il ne s'agit que d'une approximation (pas la plus pertinente d'ailleurs). Le "OUI/NON" fait penser à un QCM ; la réponse exacte figure peut-être dans les autres choix. Il s'agit de celle évoquée dans les dernières lignes de mon message précédent :

$E_{p}=\frac{1}{2}k\left(\sqrt{\left(a+x\right)^{2}+y^{2}}-a\right)^{2}+m.g.y$

$E_{p}=\frac{1}{2}k\left(\sqrt{\left(a+l.\sin\left(\theta\right)\right)^{2}+l^{2}.\left[1-\cos\left(\theta\right)\right]^{2}}-a\right)^{2}+m.g.l.\left[1-\cos\left(\theta\right)\right]$
Si, comme je le suppose, la suite de l'exercice consiste à étudier les oscillations de faible amplitude, la simplification la plus pertinente est celle que j'ai présentée dans mon message précédent :

$E_{p}\approx\frac{1}{2}k\cdot x^{2}+m.g.y\approx\frac{1}{2}k\cdot l^{2}\cdot\sin^{2}\left(\theta\right)+m.g.l.\left[1-\cos\left(\theta\right)\right]$

Posté par re : Energie potentielle ressort 05-09-17 à 14:39

Ce que tu as mis correspond bien à ce que j'avais trouvé (cf la photo de mes calculs que j'aurais du écrire). Malheureusement il n'y avait pas de suite à l'exo, et toute les autres réponses étaient fausses dimensionnellement. Enfin bon c'est ça la physique de PACES ... :/ . Mais merci beaucoup en tout cas

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Energie potentielle ressort

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique