Inscription / Connexion Nouveau Sujet
Énergie potentielle
Bonjour,
Déterminer l'énergie potentielle du système suivant:
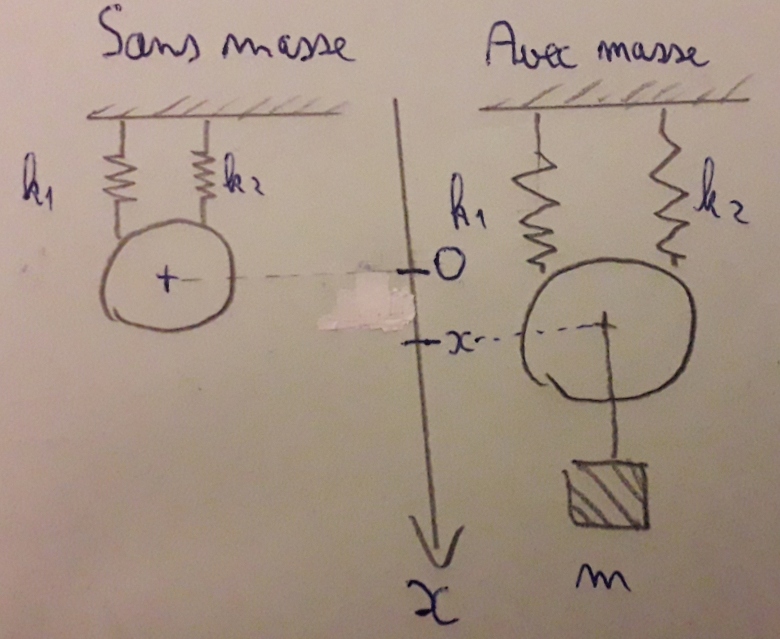
Un disque, de masse négligeable, est accroché à un plafond par deux ressort de constante k1 et k2. Une masse, de masse m, est accroché à ce disque par son centre.
L'énergie potentielle du système est la somme des énergie potentielles de chaque constituants.
Je caractérise la position de la masse par la coordonnée x et je place l'origine à la hauteur du plafond.
Je sais que l'énergie potentielle de pesanteur est U1=-m(g.r) = -mgx
Je sais que l'énergie élastique des ressorts est (1/2)kx2
J'ai du mal à déteminer cette énergie potentielle à cause de la morphologie du système.
Si quelqu'un a une idée ?
L'objectif final est de déterminer la période des petites oscillations du systèmes alors l'étude se fait lors des oscillations.
Attention à ne pas mettre du "x" à toutes les sauces...
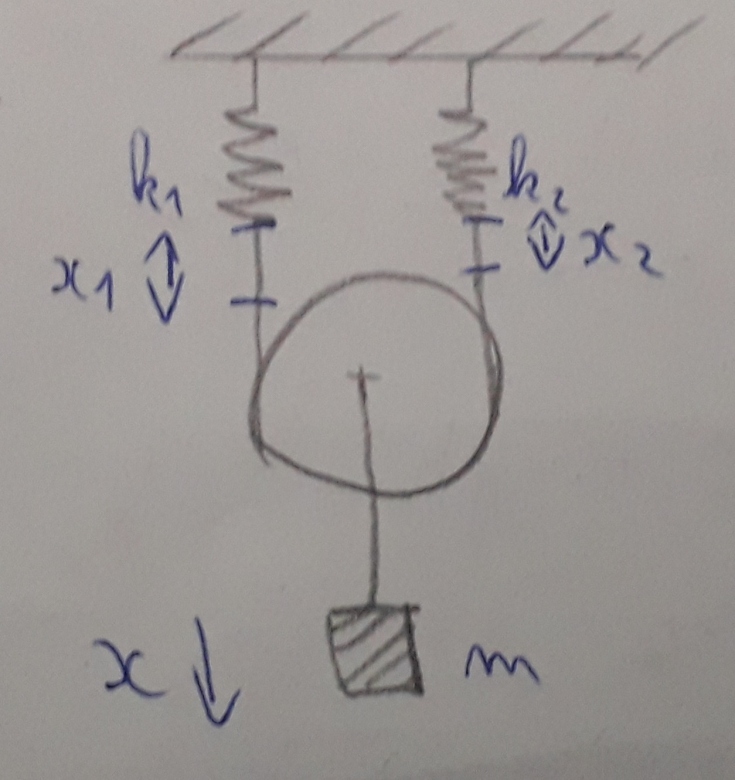
Tu peux noter x1 l'allongement du ressort n° 1 et x2 l'allongement du ressort n° 2. Que vaut alors le déplacement x du centre de la poulie si on choisit comme origine des x, la position du centre de la poulie lorsque les ressorts n'exercent aucun effort (masse m enlevée) ? Une fois ceci bien vu, la suite est assez simple.
J'ai du mal à m'imaginer le système. Notamment si disque tournes due au ressorts.
C'est vrai qu'en cours on utilise x comme un fourre tout sans prendre en compte l'élongation due à chaque ressort alors je n'ai pas l'habitude. Je n'arrive pas à placer x1 et x2 sur le schéma.
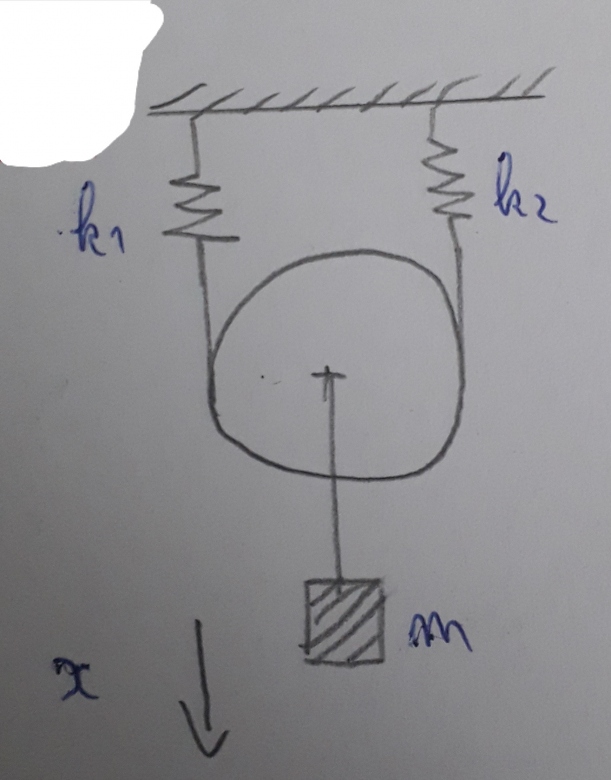
Je préfères ton schéma du haut car, pour obtenir x en fonction de x1 et x2, il va falloir raisonner sur le fait que le fil joignant les deux ressorts en passant sur la gorge de la poulie est inextensible.Sous l'effet du poids de la masse m et aussi à cause des oscillations, le point de liaison entre le ressort n°1 et le brin gauche du fil est abaissé de la distance x1 par rapport à l'absence de charge (masse m). De même le point de liaison entre le ressort n° 2 et le brin droit du fil est abaissé de la distance x2 par rapport à l'absence de charge. Dans le cas le plus général, cela engendre une rotation de la poulie autour de son axe et un déplacement vertical du centre de la poulie de "x" (cela : je crois que tu as compris). Ces notations ont l'intérêt de permettre des expressions simples des trois énergies potentielles.
J'ai introduit les constantes x1 et x2 sur le schéma.
U1=(1/2) k1 x1
U2=(1/2) k2 x2
Pour déterminer x1 et x2 je pense qu'il faut résoudre un système de deux équations à deux inconnues.
J'ai tendance à dire que x=x1+x2
Car x est le déplacement maximal de la poulie engendré par les deux
allongements des ressorts x1 et x2.
Pour la deuxième équation, je ne sais pas, peut-être introduire la constante de raideur équivalente à 2 ressorts en parallèle ?
Je dirais que pour que le système tend a être à l'équilibre, il faut que la force de tension du fil à gauche et à droite soit égale (en norme) et également la force de rappel des ressorts.
On peut écrire:
k1 x1 = k2 x2
Et finalement, je pense ne pense plus que x est le déplacement maximal. Du fait qu'il y a des oscillations x est la moyenne de xa et x2:
x=x1+x2/2
Nous voila avec deux équations à deux inconnues que l'on résout et on remplace x1 et x2 dans les formules de l'énergie potentielle d'élasticité des ressorts:
U1=(1/2) k1 x12
U2=(1/2) k2 x22
A propos de la relation entre x, x1 et x2, je me permets un conseil d'ordre général. Lorsque tu obtiens une formule littérale, tu as tout intérêt à :
1° : vérifier son homogénéité (pas de problème ici) ;
2° : tester son réalisme. Cela revient à tester la formule sur quelques cas simples physiquement évidents. Suppose x1=x2 : que vaut x ? Suppose x1=-x2 : que vaut x ? Manifestement, la formule x= x1+x2 ne convient pas.
La relation k1.x1=k2.x2 est correcte mais doit être démontrée rigoureusement dans le cadre de la dynamique puisqu'il s'agit d'étudier un oscillateur. Tu dois connaître le théorème de Koenig n° 2 portant sur le moment dynamique d'un solide : le moment dynamique de la poulie en son centre d'inertie G est le même dans le repère terrestre galiléen et dans le repère de Koenig, c'est à dire le repère d'origine G, en translation par rapport à un repère terrestre. Cela permet d'appliquer le théorème du moment dynamique en G même si G est animé d'un mouvement de translation non uniforme. Puisque la masse de la poulie est d'influence négligeable, le moment d'inertie de la poulie par rapport à son axe de rotation passant par G peut être considéré égal à zéro. On arrive ainsi à ton résultat.
Pour l'énergie potentielle : ne pas oublier celle de pesanteur.
Voici un schéma susceptible de t'aider.