Inscription / Connexion Nouveau Sujet
energie et ressort
Bonjour je suis en classe préparatoire et j'ai quelque problème avec cet exercice, je vous remercie d'avance pour votre aide 
Un bloc de masse m est abandonné sans vitesse initiale à une distance L de l'extrémité d'un ressort détendu.
Quand il s'arrête, le ressort s'est comprimé puis le bloc va remonter. On ne considère aucun frottement.
1)Déterminer la longueur dont le ressort s'est comprimé.
2)Rechercher la position pour laquelle la vitesse du bloc est maximale.
on a : K=100 N/m ; θ=30° ; L=50cm ; m=0,50 kg
je ne sais pas du tout comment commencer le problème à part qu'il faut surement utiliser le théorème de l'énergie cinétique. J'ai calculé Ep=mgL*sinθ. Je pense peut être utiliser le fait que à l'instant ou le ressort est complètement comprimé la masse est immobile et sa vitesse est nulle ?
je ne voit pas comment faire
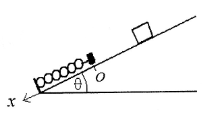
jte la fais courte ^^
le bloc arrive en O avec une énergie : EcO = 0,5*9,81*0,5*sin 30° = ... J
puis le ressort se comprime. l'énergie transmise est : 1/2.k.x² où x est la longueur dont se comprime le ressort. il se comprime jusqu'à ce que la vitesse de l'objet soit nulle (jusqu'à ce que le bloc n'ait plus d'énergie) ... mais attention car le bloc avait encore un peu de réserve d'énergie potentielle en O !
donc on a : Ec0 + mg.x.sin 30 ° = 1/2.k.x² !
une ptite équation du second degré à résoudre
désolé je n'ai pas bien démontré tout ça et je suis allé un peu vite donc si tu as des questions n'hésite pas ! mais je crois que tu étais bien parti !
ok , ça marche on trouve x=0.182m sa me parait être possible
pour la question 2 je compte utiliser:
ΔEc = Ec(f)-Ec(i) = Ec(f)-0 = 1/2mv² = 
W et obtenir v en fonction de x, tracer la fonction rechercher le maximum et le tour est joué ?
Annuler
connectez vous