Inscription / Connexion Nouveau Sujet
Energie d'un pendule
Bonjour,
J'essaye de faire un exercice mais je ne parviens pas jusqu'au bout :
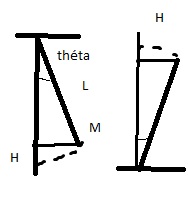
J'attache le schéma du pendule.
On considère un pendule constitué d'une tige de masse négligeable de longueur L, et d'une masse ponctuelle M fixée à son extrémité.
1. Calculer l'énergie potentielle de ce systeme en utilisant théta comme paramètre.
2.Déterminer la position d'équilibre de ce pendule et sa stabilité.
3.Que devient cette expression pour théta faible? On gardera cette hypothèse dans la suite.
4.On ajoute au centre de rotation O un ressort de torsion, ce ressort est associé à une énergie potentiel 1/2 K  ^2
^2
Donner la nouvelle valeur de l'énergie potentielle.
5.On inverse le pendule. Déterminer la nouvelle expression de lénergie potentielle. On choisira la référence en H (Position verticale de la masse)
6.Montrer que la stabilité de l'équilibre en H dépend des valeurs de K M L et g
Ce que j'ai fait :
1)Eph = mg(H-Lcos )
)
2)dEph/dt = mglsin =0
=0
 =
= ou
ou  =-
=-
d^2Ep/dt : On trouve que pour  =
= c'est stable et -pi instable.
c'est stable et -pi instable.
3)cos =1, l'expression devient : mg(H-L)
=1, l'expression devient : mg(H-L)
4)Ep=EpK + Eph
Ep= mg(H-L) + 1/2K ^2
^2
5)La je ne vois pas, selon mon dessin, la différence de hauteur pour Eph est toujours H-Pcos ,
,
et ça ne change pas mon expression
Merci de votre aide,
Arks
Bonjour Arks,
Reponse 1 : je ne comprends pas ce que represente la grandeur H dans ta reponse 1. Pour moi, H et L sont identiques, on obtiend donc Ep = mgL(1-cos ), en prenant son origine au point le plus bas atteint par M (cad
), en prenant son origine au point le plus bas atteint par M (cad  = 0).
= 0).
Reponse 2 : OK pour dEp/d = 0 pour
= 0 pour  - 0 ou
- 0 ou  , mais grosse erreur apres : lorsque
, mais grosse erreur apres : lorsque  est negatif et tend vers zero Ep diminue, et apres
est negatif et tend vers zero Ep diminue, et apres  - 0 Ep augmente ; donc Ep passe par un minimum lorsque
- 0 Ep augmente ; donc Ep passe par un minimum lorsque  passe par zero : la position d'equilibre stable est donc
passe par zero : la position d'equilibre stable est donc  = 0.
= 0.
Reponse 3 : pour  faible, cos
faible, cos
 1 -
1 -  2/2, donc Ep
2/2, donc Ep  mgL
mgL 2/2.
2/2.
Reponse 4 : ok, on additionne les deux Ep.
reponse 5 : si on veut garder  petit (demande en 3) en inversant le pendule, on est contraint de modifier la definition de
petit (demande en 3) en inversant le pendule, on est contraint de modifier la definition de  : c'est maintenant
: c'est maintenant  ' =
' =  -
-  qu'il faut prendre (
qu'il faut prendre ( ' = angle entre la tige et la verticale ascendante). Si on remplace dans l'expression de Ep obtenue en 1, on obtient Ep = mgL(1 + cos
' = angle entre la tige et la verticale ascendante). Si on remplace dans l'expression de Ep obtenue en 1, on obtient Ep = mgL(1 + cos '). Mais dans cette expression
'). Mais dans cette expression  = 0 donne Ep = 2mgL
= 0 donne Ep = 2mgL  0, puisque l'origine est encore au point le plus bas. On veut l'origine de Ep au point le plus haut, donc il faut ecrire Ep = mgL(1 + cos
0, puisque l'origine est encore au point le plus bas. On veut l'origine de Ep au point le plus haut, donc il faut ecrire Ep = mgL(1 + cos ') - 2mgL, soit Ep = mgL(cos
') - 2mgL, soit Ep = mgL(cos ' - 1). En gardant l'hypothese des petits angles, ceci devient Ep
' - 1). En gardant l'hypothese des petits angles, ceci devient Ep  -mgL
-mgL ' 2/2. L'energie potentielle de pesanteur est devenue negative en raison du choix de son origine.
' 2/2. L'energie potentielle de pesanteur est devenue negative en raison du choix de son origine.
Si on ajoute l'energie du ressort spiral, en supposant qu'il n'est pas tordu lorsque le pendule est vertical M en l'air (cad  ' = 0), on obtient finalement Ep = (k - mgL)
' = 0), on obtient finalement Ep = (k - mgL) ' 2/2.
' 2/2.
Ep ainsi ecrit est bien nul pour  ' = 0, et que cette valeur correspond a en extremum puisque Ep varie en
' = 0, et que cette valeur correspond a en extremum puisque Ep varie en  ' 2.
' 2.
Pour etudier la stabilite de cet equilibre il faut donc etudier le signe de Ep si on augmente legerement l'angle  '. Un raisonnement elementaire montre que si k > mgL l'equilibre sera stable (le ressort spiral ramene le pendule a la verticale), sinon c'est le poids qui l'emporte et le pendule descendra jusque
'. Un raisonnement elementaire montre que si k > mgL l'equilibre sera stable (le ressort spiral ramene le pendule a la verticale), sinon c'est le poids qui l'emporte et le pendule descendra jusque  ' =
' =  .
.
Cet exo a une application pratique : le metronome mecanique des apprentis musiciens.
Si tu as des question n'hesite pas a envoyer un post. Prbebo.



