Inscription / Connexion Nouveau Sujet
energie cinetique en rotation
bonjour.J'ai besoin d'aide pour resoudre cet exercise merci d'avance
deux spheres homogenes et quasi ponctuelles A et B de masse ma et mb sont reliés par une tige de masse négligeable .
L'ensemble est mobile autour d'un axe horizontal perpendiculaire a AB en son milieu O.les frottement negligés .
1.La tige partant a la position horizontale est abandonné sans vitesse initiale.
a.exprimer en fonction de g et L=AB Wmax du systeme au cours de son mvt
Bonsoir ado12,
Quelles sont tes pistes? Qu'as-tu pu faire? Quels sont les points qui te bloquent?
Il s'agit là d'un problème de mécanique  .
.
Une bonne habitude à prendre est de toujours commencer par faire un schéma, définir le système étudié et son référentiel ainsi que faire un bilan des forces  .
.
Bon courage,
Au plaisir d'échanger  .
.
Metal Oxalate
bonjour metal merci pour ta reponse
au fait j'arrive pas a determiner la vitesse angulaire maximale .j'ai fait
Ecf-Eci=Wpa+Wpb
1/2Jwmax-1/2Jwi=(ma+mb)gL/2 or wi=0 donc on aura 1/2Jwmax=(ma+mb)gL/2
mais jarrive pas a continuer
L'idée de base (conservation de l'énergie mécanique) est la bonne  .
.
En négligeant les forces de frottement, on a bien conservation de l'énergie mécanique.
En revanche, l'expression des énergies doit être corrigée  .
.
Afin de bien se comprendre, je propose d'utiliser les notations suivantes:
-  Em,i: variation d'énergie mécanique de la masse i (i = A ou B)
Em,i: variation d'énergie mécanique de la masse i (i = A ou B)
-  Ec,i: variation d'énergie cinétique de la masse i (i = A ou B)
Ec,i: variation d'énergie cinétique de la masse i (i = A ou B)
-  Ep,i: variation d'énergie potentielle de pesanteur de la masse i (i = A ou B)
Ep,i: variation d'énergie potentielle de pesanteur de la masse i (i = A ou B)
- wi: vitesse angulaire [rad/s] de la masse i (i = A ou B)
- Vi: vitesse [m/s] de la masse i (i = A ou B)
Concernant l'énergie potentielle de pesanteur (Ep):
On rappelle la relation:  Ep,i = mi.g.(Zi,final - Zi,initial)
Ep,i = mi.g.(Zi,final - Zi,initial)
=>  Ep,tot =
Ep,tot =  Ep,a +
Ep,a +  Ep,b
Ep,b
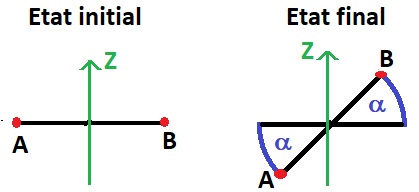
NB1: Sur le schéma en pièce jointe, on voit que si B monte (Ep,b augmente), A descend (Ep,a diminue).
Concernant l'énergie cinétique (Ec):
On rappelle la relation: Ec = 1/2.mi.Vi2
=>  Ec,tot =
Ec,tot =  Ec,a +
Ec,a +  Ec,b
Ec,b
NB2: Comme A et B sont relié par une barre, et qu'ils sont équidistant du l'axe de rotation, Va =Vb
NB3: Il existe une relation entre la vitesse V [m/s] et la vitesse angulaire w [rad/s]. Vois-tu laquelle?
Bon courage,
Metal Oxalate
merci metal pour la reponse
au fait on n'a fait l'energie cinetique en classe.J'arrive toujours pas a comprendre .
Je dois utiliser la variation de l'energie cinetique en rotation je pense car on me demande la vitesse angulaire maxi Wmax
Concernant l'énergie cinétique:
Tu as raison, il faut bien utiliser la formule en rotation.
Toutefois, la formule que tu as utilisée (E = J.w) contient une petite erreur.
J'ai alors voulu te faire redémontrer la formule, en partant de celle pour l'énergie cinétique en translation  .
.
- Ec = 1/2.mi.Vi2
- Vi = (L/2).wi (vois-tu pourquoi?)
On obtient alors: Ec = 1/2.mi.(L.wi/2)2
Donc: Ec = 1/2.[mi.L2/4].wi2
En posant Ji = mi.L2/4 (moment d'inertie de la masse i), on trouve: Ec = 1/2.Ji.wi2
Bref, il manquait le carré  .
.
Concernant l'énergie potentielle de pesanteur (Ep):
Comment es-tu arrivé à la formule "Wpa+Wpb =(ma+mb)gL/2"?
reprenons la formule de mon post d'hier soir:  Ep,i = mi.g.(Zi,final - Zi,initial)
Ep,i = mi.g.(Zi,final - Zi,initial)
Initialement, la barre est horizontale: Za,initial = Zb,initial = 0
Puis, la barre se penche. Que vaut Za,final par rapport à Zb,final?
Exprimer  Ep,tot =
Ep,tot =  Ep,a +
Ep,a +  Ep,b
Ep,b  .
.
Bon courage,
Metal Oxalate
bonjour Metale si nous revenons a notre exercice svp
je propose qu'on utilise la variation de l'energie cinetique:
∆Ec=Ecf-Eci=W(Pa)+W(Pb) or Eci=0
=1/2 J∆W²max =-MagHa+MbgHb
J∆=2/5 Ma(ra)²+2/5Mb(rb)²=2/5[Ma(L/2)²+Mb(L/2)²]=2/5(L/2)²[Ma+Mb] or Mb=3Ma
= 2/5(L/2)²[Ma+3Ma] =2/5L²/4( 4Ma) =2/5MaL²
1/2 J∆W²max=(1/2x2/5MaL²)W²max=(1/5 MaL²)W²max=-MagL/2+MbgL/2
(1/5 MaL²)W²max=L/2g(-Ma+Mb)=L/2g(-Ma+3Ma)=L/2gx2Ma= LgMa
(1/5 MaL²)W²max= LgMa donc :W²max=Lg Ma/1/5MaL²=5g/L → Wmax=√5g/L=15,8rad/s
bonjour.J'ai besoin d'aide pour resoudre cet exercise merci d'avance
deux spheres homogenes et quasi ponctuelles A et B de masse ma et mb sont reliés par une tige de masse négligeable .
L'ensemble est mobile autour d'un axe horizontal perpendiculaire a AB en son milieu O.les frottement negligés .
1.La tige partant a la position horizontale est abandonné sans vitesse initiale.
a.exprimer en fonction de g et L=AB Wmax du systeme au cours de son mvt
*** message déplacé ***
Bonjour ado12,
Es-tu en mesure de commencer par un schéma de la situation par exemple et proposer une piste que tu as en tête ?

*** message déplacé ***
bonjour gbm
ok bien noté .je n'arrive pas a faire un schema a partir de la page du forum .
Et en plus je propose qu'on utulise la variation de l'energie cinetique pour cet exo .
1/2JW²f-1/2JW²i=W(Pa)+W(Pb) or Wi=0 donc on aura :
1/2JW²f=W(Pa)+W(Pb) 'jarrive plus a continuer
*** message déplacé ***
Bonjour ado12,
Il y a du bon et du mauvais dans ce que tu as fait.
∆Ec=Ecf-Eci=W(Pa)+W(Pb) or Eci=0
- Qu'appelles-tu Pa et Pb? Point A et Point B?
- Pour l'énergie potentielle de pesanteur, le P doit être à l'exterieur de la parenthèse
 : Wp(A) et Wp(B)
: Wp(A) et Wp(B)
- Comme la lettre W est déjà utilisée pour la vitesse angulaire, on va utiliser la lettre E pour décrire l'énergie
 : Ep(A) et Ep(B)
: Ep(A) et Ep(B)
 Ec =-MagHa+MbgHb
Ec =-MagHa+MbgHb- D'où vient le signe - devant Ma.g.Ha? A ce stade, il ne devrait pas apparaitre de ce signe - (mais Ha ou Hb peut être négatif
 )
)
J∆=2/5 Ma(ra)²+2/5Mb(rb)²
- Que vient faire
 ici: "J∆"?
ici: "J∆"?
Placé devant une autre lettre, le symbole
 signifie variation. Mais placé après la lettre il ne veut rien dire...
signifie variation. Mais placé après la lettre il ne veut rien dire...
- d'où viennent les coefficient "2/5"?
or Mb=3Ma
Cette donnée n'était pas mentionné dans tes précédents message. Est-ce bien une donnée de cet exercice?
(1/5 MaL²)W²max=L/2g(-Ma+Mb)=L/2g(-Ma+3Ma)=L/2gx2Ma= LgMa
- C'est la bonne idée, il faut utiliser l'égalité
 Ec =
Ec =  Ep
Ep
- Par contre, Ha
 Hb (Ha = - Hb).
Hb (Ha = - Hb).Afin de bien se comprendre, je propose d'utiliser les notations suivantes:
- Ec,i: variation d'énergie cinétique de la masse i (i = A ou B)
- Ep,i: variation d'énergie potentielle de pesanteur de la masse i (i = A ou B)
- wi: vitesse angulaire [rad/s] de la masse i (i = A ou B)
Energie cinétique:
 Ec = Ecf - Eci. Or Ec,i = 0 (vitesse initiale nulle).
Ec = Ecf - Eci. Or Ec,i = 0 (vitesse initiale nulle).
Donc  Ec = Ecf = 1/2.(Ja+Jb).wmax²
Ec = Ecf = 1/2.(Ja+Jb).wmax²
Ji = mi.ri²
Donc Ja + Jb = ma.L²/4 + mb.L²/4
Ja + Jb = (ma+mb).L²/4
Au final, pour l'énergie cinétique on a:
 Ec = 1/2.(ma+mb).L².wmax²/4
Ec = 1/2.(ma+mb).L².wmax²/4
Energie potentielle de pesanteur:
 Ep =
Ep =  Ep(A) +
Ep(A) +  Ep(B)
Ep(B)
 Ep(A) = Ma.g.(Ha,f - Ha,i)
Ep(A) = Ma.g.(Ha,f - Ha,i)
 Ep(B) = Mb.g.(Hb,f - Hb,i)
Ep(B) = Mb.g.(Hb,f - Hb,i)
- à l'état initial, la barre est horizontale: Ha,i = Hb,i = 0
- à l'état final, comme Ma  Mb, on a: Ha = - Hb avec
Mb, on a: Ha = - Hb avec
Hb = (L/2).sin( ) [vois-tu pourquoi?]
) [vois-tu pourquoi?]
Au final, pour l'énergie potentielle de pesanteur on a:
 Ep = (Mb - Ma).g.(L/2).sin(
Ep = (Mb - Ma).g.(L/2).sin( ).
).
Au maximum, la barre se retrouve à la verticale ( = -
= - /2)
/2)
D'où:  Ep = -(Mb - Ma).g.(L/2)
Ep = -(Mb - Ma).g.(L/2)
Conservation de l'énergie mécanique:
En négligeant les pertes dues aux frottements de l'air, on a conservation de l'énergie mécanique.
 Em =
Em =  Ec +
Ec +  Ep = 0
Ep = 0
Donc  Ec = -
Ec = -  Ep
Ep
D'où:  Ec = 1/2.(Ma+Mb).L².wmax²/4 = +(Mb - Ma).g.(L/2)
Ec = 1/2.(Ma+Mb).L².wmax²/4 = +(Mb - Ma).g.(L/2)
En isolant wmax, on obtient:
wmax = 2. [(Mb - Ma).g/(L.(ma+mb))]
[(Mb - Ma).g/(L.(ma+mb))]
Je te laisse faire l'application numérique  .
.
N'hésites pas à poser des questions, si tu en as  .
.
bonjour metal je vous remercie d'avance pour le tps que vous prenez pour me repondre.
au fait dans l'enoncé j'avais oublié de mettre mb=3ma .
W(Pa):je l'appellais le travaille du poids pour le sphere A: Ma.g.ha
W(Pb):je l'appellais le travaille du poids pour le sphere B:Mb.g.hb et momoent d'inertie de la sphere= 2/5mL² d'aprés ce j'ai compris .
donc si on prend comme vous dites Ep(a)=Ma.g.ha et E(pb)=Mb.g.hb
∆ Ec=∆ Ep→Ecf-Eci=-Ma.g.ha+Mb.g.hb car hb=-ha Eci=0(etat initial) donc on aura
=1/2 JW²max =-Ma.g.Ha+Mb.g.Hb
J∆=2/5 Ma(ra)²+2/5Mb(rb)²=2/5[Ma(L/2)²+Mb(L/2)²]=2/5(L/2)²[Ma+Mb] or Mb=3Ma
= 2/5(L/2)²[Ma+3Ma] =2/5L²/4( 4Ma) =2/5MaL²
1/2 J.W²max=(1/2x2/5Ma.L²)W²max=(1/5 Ma.L²)W²max=-Ma.g.L/2+Mb.g.L/2
(1/5 MaL²)W²max=L/2g(-Ma+Mb)=L/2g(-Ma+3Ma)=L/2gx2Ma= L.g.Ma
(1/5 Ma.L²)W²max= L.g.Ma donc :W²max=L.g .Ma/1/5Ma.L²=5g/L → Wmax=√5g/L=15,8rad/s
bjr metal je viens de voir ta methode
mais je comprends tjrs pas pourquoi vous prenais Ji = mi.ri² alors que on a une sphere homogene on devrais prendre d'aprés ce que j'ai compris J=2/5mi.r²i
et en plus pourquoi vous avais pris alpha=-pi/2 au lieu de pi/2. svp si vous m'eclaicir la dessus . A part ses questions qui me trouble un peu j'ai bien compris et noté votre demarche .
Content que tu poses des questions !
C'est la bonne attitude à avoir pour progresser  .
.
Concernant le moment d'inertie:
En fait, si on reprend l'énoncé, on a "deux spheres homogenes et quasi ponctuelles A et B de masse ma et mb sont reliés par une tige de masse négligeable"
Ainsi, c'est la tige qui tourne (comme une hélice) et aux extremités de la tige il y a les sphères  .
.
Autrement dit, l'axe de rotation est perpendiculaire à la tige. Les sphères sont fixes par rapport à la tige, elles tournent avec la tige.
Si les sphères tournaient sur elles mêmes et qu'on voulait calculer leur moment d'inertie on aurait un soucis: "J = 2/5.m.r²"
r devrait alors être le rayon de la sphère. Or l'énoncé nous dit que les sphères sont ponctuelles ! Donc r = 0 !
Bref  .
.
Une autre manière de s'en convaincre est demontré la formule:
Ec,a = 1/2.ma.Va²
Va = r.w (vois-tu pourquoi?)
r = L/2
On obtient alors: Ec,a = 1/2.ma.(L.w/2)²
Donc: Ec,a = 1/2.[ma.L²/4].w²
Concernant la valeur de  ::
::
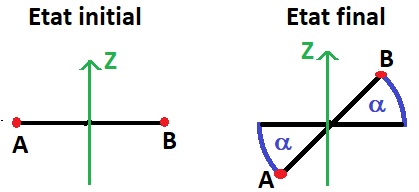
- Si on reprend mon poste du 13 décembre, l'angle  est défini par la différence d'angle entre la ligne horizontale et la position du point B.
est défini par la différence d'angle entre la ligne horizontale et la position du point B.
-  grandit dans le sens trigonométrique (anti-horaire).
grandit dans le sens trigonométrique (anti-horaire).
Comme Mb > Ma, on sait qu'à l'état final B serait en bas et A en haut  .
.
Avec un point B en bas, on a  = -
= - /2
/2
Bonjour Metal meilleurs voeux et bonne et heureuse année 2020.
je voulais ajouté une question sur notre exo. On me demande de calculer
jusqu'a quelle hauteur hmax de la sphere B va-t-elle monter avant de rebrousser chemin
je propose ceci:
1/2.(Ma+Mb).L².wmax²/4 =(Mb - Ma).g.hmax
hmax =[1/2.(Ma+Mb).L².wmax²/4 ]/(Mb - Ma).g
=[1/2.(Ma+3Ma).L².wmax²/4 ]/(3Ma - Ma).g
=[1/2.(4Ma).L².wmax²/4 ]/(2 Ma).g
= [1/2.(4Ma).L².wmax²/4 ]/(2 Ma).g =[L².wmax² ]/4.g
AN: hmax =(0.2²x10²)/(4x10)=0.1m =10cm
hmax =10cm
Re-bonjour ado12,
Puisque l'échange entre toi et krinn m'a incité à regarder tes précédents échanges, je te rappelle également que le multipost n'est pas toléré :
Bonjour gbm meilleurs voeux 2020
Je m'excuse d'abord du mal entendu avec krinn mais je trouve que ses reponse etait un peut dure .
Sur le sujet que j'avais posé avec lui certe j'ai vu un sujet semblable qui n'avait pas aboutie mais le schema n'etais pas la meme avec mon sujet que je voulais traiter.Mais ne vous enfaites pas j'adhère parfaitement a votre logique de propose d'abord avant d être guidé.et c'est ce que j'ai toujours fait d'ailleurs mais l'autre fois qu'a même avec krinn la maniere etais un brutale qu'a meme .Mais je m'excuse mon but n'etais pas de faire du mal.
par contre j'ai eu a traite avec d autres correcteurs sa c'est hyper bien passé l'explication etait top.
Je vous remercie et vous souhaite bonne journée.
ado12,
Je te remercie pour ces éléments de clarifications. J'ai vu que tes autres échanges c'étaient bien passées, je pense qu'il y a eu qu'une incompréhension entre vous : ce serait bien que tu présentes tes excuses à krinn sur l'autre topic et que vous repreniez l'échange en faisant table rase du passé.
Attention donc à la qualité rédactionnelle pour exposer ton raisonnement, cela évite les incompréhensions et tu as tous les utilitaires pour poster un schéma ou pour écrire de façon lisible des formules mathématiques.
A mon tour de t'adresser mes meilleurs voeux pour 2020 et bonne journée !
OK merci gbm .
je suis nouveau sur ce forum et je ne maitrise pas encore comment faire rentrer les signes mathematiques .je suis obligé de faire mes exo sur word et de faire un copie collé.
OK, tout est expliqué dans la FAQ (cf. les rappels dans le topic [A LIRE AVANT D'AGIR] Rappel des règles).
Tu sembles savoir comment ajouter un schéma.
Pour les formules mathématiques, c'est expliqué dans ce raccourci (clique dessous) :
 extrait de
extrait de Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?
Il faut également penser à aérer un calcul détaillé ligne après ligne, pour faciliter sa lisibilité

 moteur de recherche
moteur de recherche page de choix du forum
page de choix du forum fiches du site
fiches du site ) :
) :
 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum
