Bonjour,
J'ai un exercice d'électrostatique à préparer mais je bloque sur certaines questions et j'aurais besoin d'un peu d'aide, voici l'énoncé:

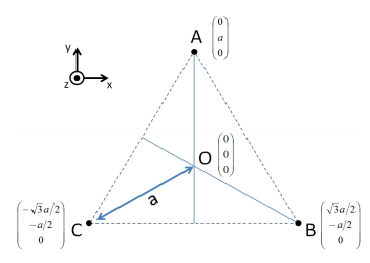
3 charges ponctuelles fixes Q, positives, sont placées au sommet d'un triangle équilatéral de centre
O, dans le plan (x,O,y), voir figure ci-dessous. On désire calculer le champ électrique généré par ces 3
charges le long de l'axe z, passant par O et perpendiculaire au plan (x,O,y), c'est à dire calculer le
champ électrique �(M) en tout point M de l'axe (Oz), situé à une hauteur z au dessus de O. On donne
dans la figure suivante les coordonnées dans la base cartésienne des trois sommets du triangle
équilatéral. On note a la distance OA=OB=OC.



1) Décrire les plans de symétrie du système passant par tout point M, situé sur l'axe z. En
déduire l'orientation du champ électrique en tout point M de l'axe z.


2) Par un raisonnement analogue déduire la valeur du champ électrique au point O.


3) Expliquer à l'aide d'un raisonnement qualitatif (avec les mains), pourquoi on peut s'attendre
à ce que le module du champ électrique généré   sur l'axe z par les 3 charges, passe par une
valeur maximale à une hauteur précise au dessus du point O.


4) Rappeler l'expression reliant le champ et le potentiel électrostatique. Justifier alors le fait
que le potentiel électrostatique sur l'axe z passe par un maximum au point O.


5) Calculer le champ électrique produit en un point M quelconque, situé sur l'axe (Oz) à une
hauteur z au dessus de O, en fonction de z, q, a et d'autres constantes.


6) Déterminer en fonction de a, la hauteur zmax pour laquelle le champ électrique généré sur
l'axe z est maximal.

7) Donner l'expression du champ électrique maximal Emax produit au point de l'axe (Oz) situé à
la hauteur zmax, en fonction de q, a et d'autres constantes.

8) Calculer le potentiel électrostatique en un point M quelconque, situé sur l'axe (Oz) à une
hauteur z au dessus de O, en fonction de z, q, a et d'autres constantes.



1->Je sais que les plans de symétrie se coupent sur l'axe z et donc que le  champ électrique s'y trouve.

2-> Si z est nul alors les champs créés par les charges A,B et C s'annulent et le champ électrique au point O vaut 0.

3-> Le champ électrique au point O est nul puis augmente lorsque z augmente, à partir d'une hauteur zmax celui-ci diminue: le champ atteint donc sa valeur maximale au point zmax.

4-> = - V

j'ai pensé à: V= ce qui ferait que si z=0 alors V est à son maxmium, mais je ne suis pas du tout certain de la réponse.

5-> =  


= .

Mais dans ce cas si z=0 le champ n'est pas nul donc je me suis forcément trompé.

Je bloque sur cette question et je ne sais trop quoi faire, pouvez-vous m'aider? Merci d'avance!