Niveau maths sup

Electrostatique: Loi de Coulomb

Posté par
Panter16 21-04-19 à 17:49

Bonjour tout le monde,

Je me suis penché sur un exercice que j'ai trouvé dans le bouquin précis électrostatique MPSI, je l'ai refait plusieurs fois mais je ne trouve pas le même résultat que le bouquin propose, voici l'exercice:

Citation :
Deux charges opposées $+q$ et $-q$ sont placées aux points $A$ et $B$ de l'axe $Oy$ tels que $\overrightarrow{OA}=-\overrightarrow{OB}=a\overrightarrow{u_y}$ avec $a$ un réel.
Déterminer la force subie par une charge $Q$ placée en un point $M$ tel que $\overrightarrow{OM}=x\overrightarrow{u_x}$
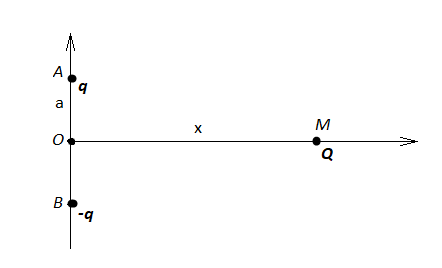
Electrostatique: Loi de Coulomb

La charge $Q$ subie deux forces:
Une exercée par la charge $q$ :

$\overrightarrow{F}_{A\to M}=\dfrac{qQ}{4\pi\epsilon_0 AM^2}\overrightarrow{u_{AM}}}=\dfrac{qQ}{4\pi\epsilon_0 AM^3}\overrightarrow{AM}}$

Une autre exercée par la charge $-q$ :

$\overrightarrow{F}_{B\to M}=\dfrac{-qQ}{4\pi\epsilon_0 BM^2}\overrightarrow{u_{BM}}}=\dfrac{-qQ}{4\pi\epsilon_0 BM^3}\overrightarrow{BM}}$

La force totale subie par $Q$ est donc:

$\overrightarrow{F}=\overrightarrow{F}_{A\to M}+\overrightarrow{F}_{B\to M}=\dfrac{qQ}{4\pi\epsilon_0 AM^3}\overrightarrow{AM}}+\dfrac{-qQ}{4\pi\epsilon_0 BM^3}\overrightarrow{BM}}$

En appliquant le théorème de Pythagore: $AM=BM=\sqrt{x^2+a^2}$

Donc:   $\overrightarrow{F}=\dfrac{qQ}{4\pi\epsilon_0 AM^3}\overrightarrow{AM}}+\dfrac{-qQ}{4\pi\epsilon_0 BM^3}\overrightarrow{BM}}=\dfrac{qQ}{4\pi\epsilon_0 (\sqrt{x^2+a^2})^3}(\overrightarrow{AM}-\overrightarrow{BM})=\dfrac{qQ}{4\pi\epsilon_0 (\sqrt{x^2+a^2})^3}\overrightarrow{AB}$

Enfin, en sachant que: $\overrightarrow{AB}=-2a\overrightarrow{u_y}$

On déduit:   $\boxed{\overrightarrow{F}=\dfrac{-aqQ}{2\pi\epsilon_0 (\sqrt{x^2+a^2})^3}\overrightarrow{u_y}}$

Le résultat du bouquin:   $\boxed{\overrightarrow{F}=\dfrac{2kqQ}{ (\sqrt{x^2+a^2})^3}\overrightarrow{u_x} \text{ avec } k=\dfrac{1}{4\pi\epsilon_0}}$

Lequel est correct?

D'avance merci!

Posté par re : Electrostatique: Loi de Coulomb 21-04-19 à 18:56

Bonsoir
Ton résultat est correct. Celui de ton corrigé est faux pour au moins deux raisons :
1° : Le résultat n'est pas homogène ! (Énorme erreur : il faut toujours vérifier l'homogénéité d'un résultat littéral, cela permet de repérer d'éventuelles fautes de calculs)
2° : Un rapide raisonnement sur les plans de symétrie, accompagné au besoin d'un schéma, montre que le vecteur force a nécessairement la direction et le sens du vecteur ( $-\vec{u_y}$ ) .

Posté par re : Electrostatique: Loi de Coulomb 22-04-19 à 10:09

Bonjour Vanoise,
Merci beaucoup!
Et oui, il fallait vérifier l'homogénéité; très important

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Electrostatique: Loi de Coulomb

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique