Bonjour attention à ta formule. Seule une différence de potentiel a un sens physique. Il faut donc choisir correctement le potentiel nul.
Sinon,tu peux calculer les deux composantes cartésiennes du vecteur déplacement et utiliser la définition classique du produit scalaire.

Pour l'angle entre 2 vecteurs : le produit scalaire de deux vecteurs peut s'exprimer en fonction des deux normes et du cosinus de l'angle entre les deux.

Bonjour et merci.

Pardon.  
Je voudrais un schéma pour appréhender les données.
Merci encore.

D'accord avec ta dernière formule sous réserve que le symbole "" désigne bien une variation. Pour être plus clair : soit un déplacement d'un point A à un point B dans un champ électrique uniforme, la variation de potentiel au cours du déplacement est :



Pour la figure, si tu places le point A à l'origine du repère, les coordonnées de B sont :

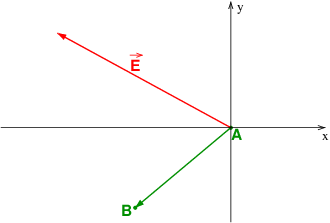
L'expression : "a une orientation de 220° dans le plan xy" n'est pas très claire. J'ai considéré que l'angle entre l'axe (Ox) et le vecteur déplacement vaut 220°.

Merci c'est plus clair pour moi.

Bonsoir,
Et merci encore.
La d.d.p. cherchée est  .
Car l'angle entre les vecteurs de notre produit scalaire, qui est une tension, est 68,6°.
E=0,626 V/m et d=0,0385m .
Merci.

Tu n'as pas tenu compte de mes messages précédents. Je récapitule les valeurs des composantes cartésiennes des vecteurs :

1° : vecteur champ électrique :



2° : vecteur déplacement (en mètre):



Différence de potentiel (en volts) :


Je ne fais qu'utiliser la relation de définition du produit scalaire...

Erreur de frappe dans mon dernier message : E_x=-550V/m et non -350V/m mais cela ne change rient à la méthode.
Tu peux aussi utiliser une autre expression du produit scalaire :


avec pour l'angle entre les deux vecteurs :



Les deux méthodes conduisent à la même différence de potentiel entre les points A et B. Il n'est pas nécessaire de calculer "d" mais tu arrives tout de même au résultat correct.

Merci beaucoup.