Niveau maths spé

Electrostatique

Posté par
Lore23 14-08-23 à 19:30

Bonsoir,

Je n'ai pas compris un point sur l'électrostatique qui retombe dans pas mal d'exos.
Par exemple, si l'on considère une distribution de charges volumique $\rho(r)$ dans une symétrie sphérique de centre $O$ et de rayon $R$ (en admettant que l'on applique le théorème de Gauss pour $r<R$ ), pour calculer la charge intérieure je me sers du fait que $dq = \rho(r) d \tau$ .
La chose que je ne comprends pas, c'est qu'en intégrant sur le volume de la sphère, $Q_{\text{intérieure}} = \rho(r) 4 \pi r^2 dr$ .

Pourquoi n'intègre-t-on pas la composante en $r$ qui est censée apparaître dans le $d\tau$ en ayant pour intégrale $\int_{r}^{r+dr} \rho(r') r'^2 dr'$ ?

Quelqu'un peut-il m'éclairer?

Posté par re : Electrostatique 14-08-23 à 20:55

Bonsoir

$\rho(r)4\pi r^{2}dr$ représente la charge élémentaire contenu entre la sphère de rayon r (r<R) et la sphère de rayon (r+dr). Pour avoir la charge contenu à l'intérieur de la sphère de rayon R, il faut intégrer entre zéro et R :

$Q_{int}=\int_{0}^{R}\rho(r)4\pi r^{2}dr$

Ta dernière expression : $\int_{r}^{r+dr}\rho(r')r'^{2}dr'$ n'a pas de sens. C'est un peu comme si tu écrivais en math :

$\\ \int_{x}^{x+dx}f(x').dx'$ ...

As-tu bien compris la signification du « d » dans dr ou dx ?

Posté par re : Electrostatique 14-08-23 à 21:15

Pour moi, le $d$ représente un élément infinitésimal.

C'est juste qu'en intégrant avec le $d \tau$ sur le volume de la sphère, j'ai du mal à voir que de la triple intégrale, on intègre seulement les composantes en $d \theta, dz$ en laissant de côté le $r^2 dr$ .

Pourtant ça me paraît logique que $Q_{\text{int,tot}} = \int_{0}^{R} ...$ puisqu'on intègre sur tout le rayon

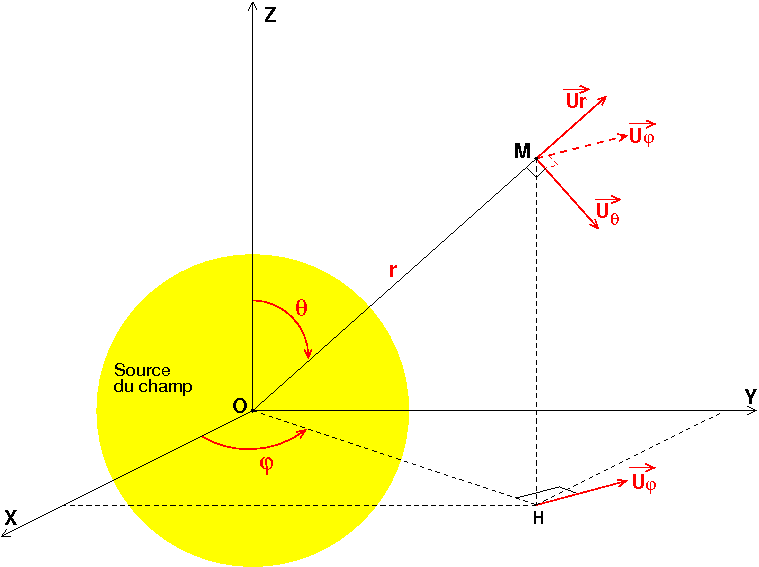
Posté par re : Electrostatique 14-08-23 à 21:50

Je veux bien te détailler le calcul. Je pars de l'expression du volume élémentaire :

$d\tau=dr.rd\theta.r\sin\left(\theta\right).d\varphi=d\varphi.\sin\left(\theta\right)d\theta.\rho_{(r)}.r^{2}.dr$

Je te fournis un schéma pour bien clarifier les notations. Maintenant, il faut bien voir que, pour couvrir la boule entière de rayon R, il faut intégrer de 0 à 2 et de 0 à seulement :
$\\ Q_{int}=\int_{0}^{2\pi}d\varphi.\int_{0}^{\pi}\sin\left(\theta\right)d\theta.\int_{0}^{R}\rho_{(r)}.r^{2}.dr=4\pi.\int_{0}^{R}\rho_{(r)}.r^{2}.dr$

Qu'est ce qui te gêne exactement ?

Electrostatique

Posté par re : Electrostatique 14-08-23 à 22:09

Merci d'avoir pris le temps de clarifier,

Je pensais que $dq = \rho(r) d\tau$ et donc en intégrant on avait $Q_{\text{int}} = \iint_V dq = \iiint_V \rho(r) d \tau = \int_{0}^{\pi} \sin \theta d \theta \int_{0}^{2\pi} d\varphi \int_{r}^{r+dr} \rho(u) u^2 du$ puisque l'on regardait le volume compris entre $r$ et $r+dr$

Ici, vous m'avez donné le cas spécifique pour $r=R$ mais je crois avoir compris le principe.

Si j'ai bien compris, mon intégrale en fonction de $du$ n'a pas de sens physique puisque ça doit être l'élément infinitésimal radial qui doit apparaître dans l'intégrale.

Dans mon cours, $Q_{\text{int}}$ ne représente pas spécifiquement la charge volumique intérieure totale (de 0 à $R$ ) mais j'y vois un peu plus clair avec les calculs maintenant.

J'avais le même problème quand j'avais fait un DS sur le sujet Centrale 2019 MP Physique-Chimie 1 s'agissant de la partie quantique à la question 15 quand il fallait exprimer la probabilité $dP$ entre $r$ et $r+dr$ (cf. https://www.doc-solus.fr/prepa/sci/adc/pdf/enonces.pdf/2019/MP_PHYSIQUE_CENTRALE_1_2019.enonce.pdf)

Posté par re : Electrostatique 14-08-23 à 22:40

Dans l'application du théorème de Gauss, entre autres situations, tu as effectivement besoin de trouver la charge contenue à l'intérieur d'une sphère de rayon r, avec r : valeur quelconque comprise entre 0 et R. Cela donne :

$Q_{int}=\int_{0}^{2\pi}d\varphi.\int_{0}^{\pi}\sin\left(\theta\right)d\theta.\int_{0}^{r}\rho_{(r')}.r'^{2}.dr'=4\pi.\int_{0}^{r}\rho_{(r')}.r'^{2}.dr'$

Posté par re : Electrostatique 14-08-23 à 22:55

Ok merci pour l'aide précieuse en tout cas

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Electrostatique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique