Inscription / Connexion Nouveau Sujet
Électrostatique
Bonjour, j'ai un exo que je ne comprends pas vraiment.
Merci d'avance. 
La charge volumique électronique dans l'atome d'hydrogène (H) peut être représentée par
l'expression :
Où a0 = 52,9 pm est le rayon de Bohr et r la distance du point considéré au centre de l'atome.
Calculer C pour que caractérise bien la distribution de charge -e de l'électron.
Bonjour
L'atome H peut se modéliser par une charge ponctuelle centrale fixe au centre du repère : un proton de charge +e. Ce proton est entouré d'un électron en mouvement rapide et désordonné. C'est cet électron en mouvement désordonné que l'on assimile à une distribution volumique de charge. Il faut donc que la charge totale dans tous l'espace entourant le noyau soit égale à -e :
Cela va te permettre d'obtenir la valeur de C.
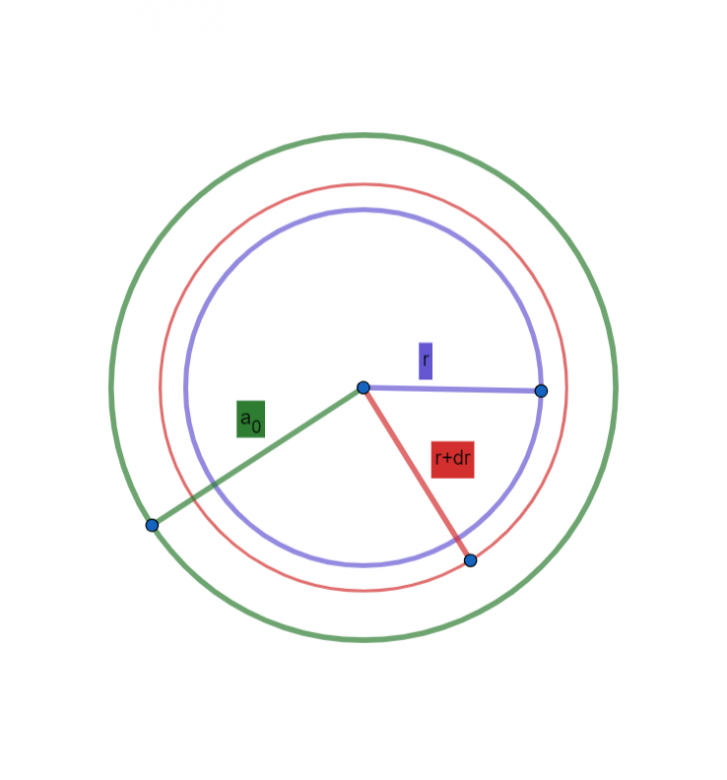
Il est possible ici de se ramener à un calcul d'intégrale simple. En effet : la densité volumique de charge ne dépend que de r : la distribution de charge admet donc le centre O du repère comme centre de symétrie. On peut s'intéresser à la charge comprise entre la sphère de rayon r et celle de rayon (r+dr). Le volume entre ces deux sphères est le produit de l'aire de la surface de la sphère par l'épaisseur dr entre les deux sphères. Cette charge élémentaire est donc :
Comme déjà expliqué, la charge totale correspondant au nuage électronique est celle d'un électron :
Cela permet d'obtenir l'expression de la constante C.
Pourquoi est ce que la densité volumique de chage ne dépend que de r ?
Comme çà ?
Ensuite j'essaie de retrouver le résultat : ..
sur les trois coordonnées sphériques : r, 
et 
, l'expression fournie de la densité volumique de charge fait intervenir seulement la coordonnée "r".
4
.r2.dr représente bien le volume élémentaire entre la sphère de centre O et de rayon r et la sphère de même centre et de rayon (r+dr).
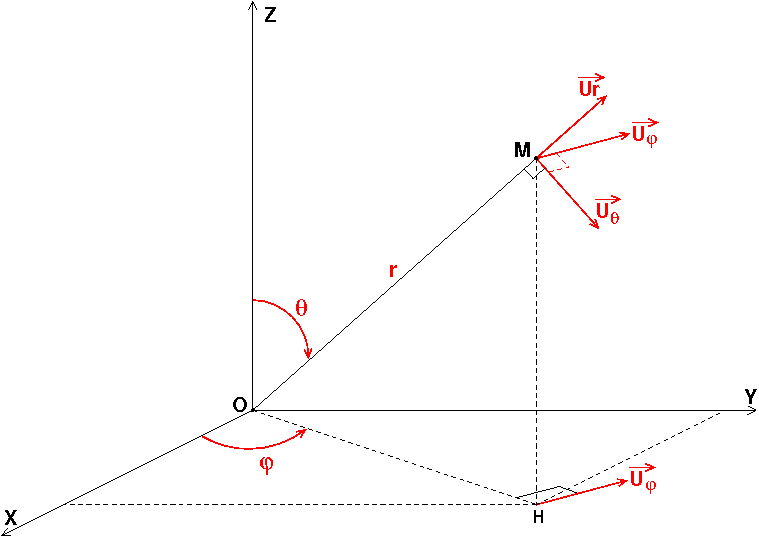
Rappel si besoin des coordonnées sphériques d'un point M quelconque de l'espace :
Le volume entre ces deux sphères est le produit de l'aire de la surface de la sphère par l'épaisseur dr entre les deux sphères
d'accord mais je n'ai pas compris pourquoi vous avez mis
Ah je vois ; la densité volumique avec dq = élément de charges et dv élément de volume.
Comme on cherche C tel que r caractérise bien la distribution de charge -e de l'électron. On va tirer l'expression de dq.
Ta dernière ligne est correcte mais écrire dq=-e est une véritable horreur. dq représente la charge comprise entre les sphères de rayons r et (r+dr).
Reste donc le calcul intégral. Tu as sans doute étudié en math l'intégration par parties...
Annuler
connectez vous