Inscription / Connexion Nouveau Sujet
électrostatique
Bonjour,
Un segment de droite AB de longueur 2L, porte une densité linéique charges λ( >0) uniforme. Soit P un point de l'espace.
>0) uniforme. Soit P un point de l'espace.
1)Déterminer l'expression du champ électrostatique élémentaire créé en P par un élément dx de la distribution.
2)Donner la valeur du champ en un point P sur l'axe Oy.
3)En déduire le champ créé par une droite infinie.
4)Vérifier que l'expression obtenue pour le champ E est compatible avec le résultat que
l'on obtient dans le cas où Y>>L.
1)dq= dx; dE(M)=k*dq/dr(x,y)² u avec dr la distance séparant le fil du point P et u corespond au vecteur unitaire partant du fil et se dirigeant vers P.
dx; dE(M)=k*dq/dr(x,y)² u avec dr la distance séparant le fil du point P et u corespond au vecteur unitaire partant du fil et se dirigeant vers P.
2) dE(P)=k*dq/y² v avec v=yey donc E=k 2L/y ey
2L/y ey
Je ne suis pas trop sûr.
Hello
Avant de partir dans un calcul inutilement complexe par rapport à ce qui est attendu.
Es tu certain que les points O (origine de l'axe Oy) et A (extrémité du segment chargé) sont confondus?
(O ne serait il pas le milieu de AB ? )
on peut le mettre où on veut
le désigne le point O? euh ... P appartient à Ox qui est perpendiculaire a AB, donc la position de O par rapport à AB va avoir une importance cruciale sur 1/ l'éventuelle symétrie du système 2/ la complexité du calcul
Et tu ne l'as justement pas mis n'importe où puisque tu l'as placé en A

On confirme O en A?
O doit se trouver sur l'axe des x, on peut alors le placer où on veut sur cet axe.
Oui, il serait préférable de le mettre au milieu du segment AB pour simplifier les calculs.
Je refais avec l'origine au milieu du segment AB:
1)dE(P)=k*dq/y2 ey avec y la distance OP
2)E=k *2L/y2 ey
*2L/y2 ey
Ah oui, je réfléchissais uniquement à partir de l'origine.
1) principe de superposition: dE(P)=dEg(M)+dEd(M) (g:gauche; d:droite)
ug+ud=2sin ey
ey
dE(M)=2ksin dq/(x2+y2)ey
dq/(x2+y2)ey
1) Principe de superposition: dE(P)=dEg(M)+dEd(M) (g:gauche et d:droite).
dEg(P)=kdq/r² ug et dEd(M)=kdq/r² ud avec r=(x²+y²)1/2
ug+ud=2sin( ) et sin(
) et sin( )=y/r
)=y/r
Ainsi, dE(P)=2ky dx/(x²+y²)3/2
dx/(x²+y²)3/2
2)E(P)=2ky
 L-Ldx/(x²+y²)3/2
L-Ldx/(x²+y²)3/2
E(P)=2ky [x/y²(x²+y²)1/2]L-Ley
[x/y²(x²+y²)1/2]L-Ley
E(P)=4ky L/y(L²+y²)1/2ey
L/y(L²+y²)1/2ey
Hello
suis un peu à la bourre ce soir (l'île c'est l'usine ...) . Que d'autres n'hésitent surtout pas à prendre la main pour t'aider (sinon j'aurai plus de temps demain)
A vue de nez
Question 2: il me semble que tu doubles la composante dEy pour tenir compte de la symétrie, dans ce cas il ne faut plus intégrer de -L à +L, mais de 0 à L 
le fois 2 se reporte dans les questions suivantes, attention donc
A vue de nez encore dans la question 4) le second membre n'est pas homogène à un champ
Bonsoir dirac
Je veux bien prendre le relais ; à charge de revanche....
Bonsoir lseioz
Comme l'a très bien dit dirac, il est primordial de commencer par étudier les plans de symétrie de la source contenant le point P où on cherche à déterminer le vecteur champ. Très souvent, cela permet d'obtenir la direction du vecteur champ sans aucun calcul.
Ici, le plan (Oxy) contient P et est plan de symétrie pour la distribution de charge : Le vecteur champ en P appartient à ce plan.
Si O lest le milieu de AB, le plan (Oyz) contient le point P et est aussi plan de symétrie ; le vecteur champ en P appartient aussi à ce plan. Pour appartenir simultanément à ces deux plans de symétrie, le vecteur champ en P est donc dirigé suivant (Oy). Inutile donc de perdre son temps à prendre deux charges élémentaires symétriques : il suffit d'exprimer le vecteur dE en p et de ne retenir que la composante suivant (Oy).
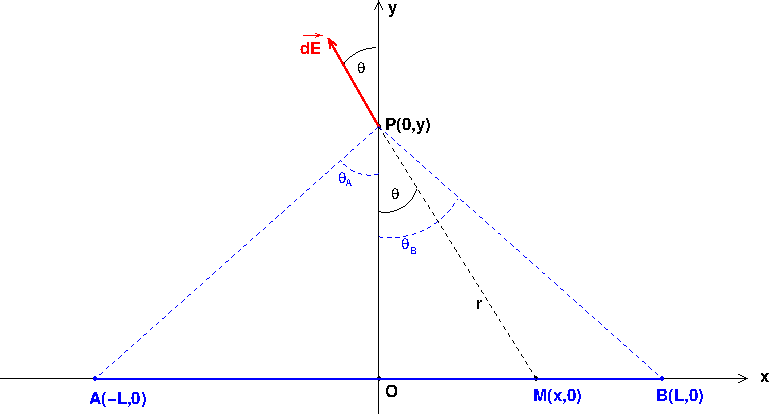
Petite astuce pas obligatoire : il peut être intéressant de faire intervenir l'angle  =(OMP) comme variable de position. Cela simplifie le calcul intégral et permet une extrapolation évidente au cas de la tige de longueur infinie.
=(OMP) comme variable de position. Cela simplifie le calcul intégral et permet une extrapolation évidente au cas de la tige de longueur infinie.
Un petit schéma pour illustrer mon message précédent. De façon immédiate :
La charge élémentaire centrée en M peut donc s'écrire, en utilisant la différentielle de l'expression précédente :
de plus :
Je te laisse simplifier : tu vas obtenir une intégrale qui se calcule “de tête” ! Reste ensuite, si cela est demandé par l'énoncé, à exprimer en fonction de y et de L.
Merci vanoise, je te "laisse la main" sur ce post ... tu as très solidement posé le cadre et les premiers jalons 
Bonjour,
1)Déterminer l'expression du champ électrostatique élémentaire créé en P par un élément dx de la distribution.
Il faut quand même utiliser le principe de superposition, même s'il est évident qu'il n'y aura que la composante ey ?
Mon résultat est-il bon ? Faut-il donner le vecteur pas la norme ?
dE(P)=2*k*y*dq/(x2+y2)3/2 ey
2)Donner la valeur du champ en un point P sur l'axe Oy.
dEy(P)=dE.cos avec dE=kdq/r2
avec dE=kdq/r2
dq= dx or x=y*tan(
dx or x=y*tan( ) donc dq=
) donc dq= y/cos2(
y/cos2( ) d
) d
Également, r=(x2+y2)1/2=y/cos
Vu que dEy(P)=dE.cos =k
=k cos
cos /y d
/y d . Ainsi sa primitive est k
. Ainsi sa primitive est k sin
sin /y d
/y d .
.
Pour les bornes d'intégration: de 0 à L soit de  =0 à
=0 à  =
= B=arctan(L/y)
B=arctan(L/y)
3)En déduire le champ créé par une droite infinie.
arctan(+ )=
)= /2 et sin(
/2 et sin( /2)=1
/2)=1
Donc E=k /y
/y
4)Vérifier que l'expression obtenue pour le champ E est compatible avec le résultat que l'on obtient dans le cas où Y>>L.
arctan(0)=0 et sin(0)=0 donc quand y>>L le champ E est nul.
Bonjour
1° : le vecteur champ élémentaire créé en P par la charge élémentaire centrée en M est colinéaire au vecteur MP (voir figure) ; son expression la plus générale est :
avec :
2° : Il faut commencer par faire le raisonnement sur les plans de symétrie (très important !) qui conduit à ne conserver que les composantes suivant y. Soit tu continues à utiliser les coordonnées cartésiennes, soit tu utilises la variable angulaire. Dans ce cas, mes messages précédents conduisent à :
avec :
(ce que tu as obtenu). En intégrant de A à B :
puisque :
.
3°: il suffit de faire tendre vers
. Je te laisse rectifier. Le résultat est très simple et pourrait être vérifié simplement par application du théorème de Gauss.
4° : Il est exact que si y tend vers l'infini avec L finie, le point P devient très éloigné de la source de champ et le vecteur champ tend vers le vecteur nul. Je pense cependant que le concepteur de l'énoncé a autre chose en tête en écrivant y>>L et non “y tendant vers l'infini”. Si y>>L, le segment de droite chargée se comportent sensiblement comme une charge ponctuelle Q égale à la charge totale de (AB) placée au centre O. A toi de vérifier.
Je te laisse réfléchir.
Merci beaucoup pour les questions 1 et 2, c'était très clair.
3) Une droite infinie signifie L>>y (ou bien  B=
B= /2) ainsi Ey=2k
/2) ainsi Ey=2k /y.
/y.
Je n'ai pas eu beaucoup d'occasions pour m'entraîner sur le théorème de Gauss,
Le cours dit : Flux=
 (intégrales fermées de la sphère de Gauss)E.dS=qintérieur/
(intégrales fermées de la sphère de Gauss)E.dS=qintérieur/ 0.
0.
q/ 0=E.4
0=E.4 r² donc E=q/4
r² donc E=q/4 r²
r² 0=kq/r². Je ne vois pas comment retrouver ce résultat.
0=kq/r². Je ne vois pas comment retrouver ce résultat.
4)y>>L : Ey=2k L/y² Lorsque l'on se place très loin, nous pouvons appliquer la relation du champ électrostatique c'est-à-dire E=kq/r². Ici nous assimilerons le segment chargé à une charge ponctuelle de charge 2
L/y² Lorsque l'on se place très loin, nous pouvons appliquer la relation du champ électrostatique c'est-à-dire E=kq/r². Ici nous assimilerons le segment chargé à une charge ponctuelle de charge 2 L et la distance r² à y².
L et la distance r² à y².
Tout me semble correct. Quelques compléments sur le théorème de Gauss. Il faut commencer par étudier les symétries de la source ; aux remarques déjà faites, on peut ajouter celle-ci : puisque la tige chargée est de longueur infinie, le plan contenant le point P où on cherche à obtenir le vecteur champ, perpendiculaire à la tige, est aussi plan de symétrie. Le vecteur champ est donc radial.
Il faut ensuite étudier les invariances de la source : invariance par rotation autour de la tige et invariance par translation parallèlement à la tige ; cela permet d'affirmer que, en tout point de l'espace autour de la tige, le vecteur champ ne dépend que de la distance à la tige : y.
On peut donc appliquer le théorème de Gauss à une surface fermée : un cylindre de hauteur h arbitraire et de rayon R=y.
Le flux à travers les disques "fermant" le cylindre est nul : vecteur champ perpendiculaire en tout point au vecteur surface.
Le flux à travers la surface latérale s'obtient aisément puisqu'en tout point de cette surface, le vecteur champ est colinéaire au vecteur surface et garde une norme constante. Le flux du vecteur champ s'écrit ainsi :
Je te laisse terminer et vérifier la cohérence avec le résultat précédent.
Pour plus de renseignements sur les influences des symétries et des invariances de la sources, tu peux consulter le document suivant, en laissant tomber ce qui concerne le magnétisme pour l'instant.
![]()
Le vecteur champ est donc radial.
Je ne me souviens plus ce que signifie radial, cela veut dire orthogonal ?
J'ai compris le raisonnement sauf le point suivant:
Je sais que dans un produit scalaire, si 2 vecteurs sont orthogonal alors le produit est nul mais je n'arrive pas à me visualiser pourquoi le vecteur champ électrostatique est le vecteur nul à travers les disques fermant le cylindre de Gauss.
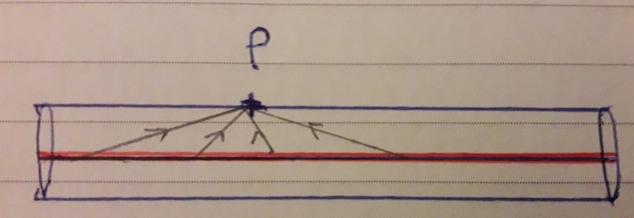
Est-ce correct la représentation du champ électrostatique ci-joint avec la droite rouge étant la droite chargé ?
Et comment justifier de sortir le "E" de l'intégrale, il faudrait qu'il soit constant en direction, sens, norme. Peut-être que j'ai mal assimiler la notion de champ, est-ce "une somme de vecteurs" ?
Je raisonne en utilisant les coordonnées cylindriques définies sur mon document au paragraphe V.2.
Je ne me souviens plus ce que signifie radial
Colinéaire à
Concernant le théorème de Gauss :
1° flux à travers les disques de base : le vecteur champ n'est pas connu mais on sait qu'il est colinéaire à
2° flux à travers la surface latérale. Son expression générale est :
En tout point de la surface le vecteur champ est radial donc colinéaire au vecteur surface :
L'étude des invariances montre que E dépend de r mais pas de z et
 . Le vecteur champ garde donc une norme fixe en tout point de la surface latérale :
. Le vecteur champ garde donc une norme fixe en tout point de la surface latérale :
Est-ce correct la représentation du champ électrostatique ci-joint avec la droite rouge étant la droite chargé ?
Dans le cas limite du fil de longueur infinie, la somme de tous les vecteurs champ élémentaire