Inscription / Connexion Nouveau Sujet
électrostatique
Bonjour les amis,
J'ai un souci par rapport à une problématique de l'électrostatique.Il s'agit de calculer le champ électrique crée par un segment AB chargé par une densité linéique uniforme continue en passant en premier lieu obligatoirement par le calcul du potentiel électrostatique.
Voici ce que j'ai pu trouver:
=
+K
par calcul direct du champ électrique j'ai trouvé ceci
et par utilisation E=-grad(V), selon ez ,j'ai trouvé des résultats cohérents.
Qu'est ce que vous en pensez?
Merci d'avance
Bonjour
Pourrais-tu poster un scan du schéma afin de bien préciser tes notations ?
En quels points de l'espace détermines-tu le vecteur champ et le potentiel. Il y a deux cas simples :
1° :le point M où on fait le calcul appartient à la droite contenant le segment AB ;
2° : le point M appartient à la médiatrice de (AB)
En dehors de ces points le calcul est très délicat...
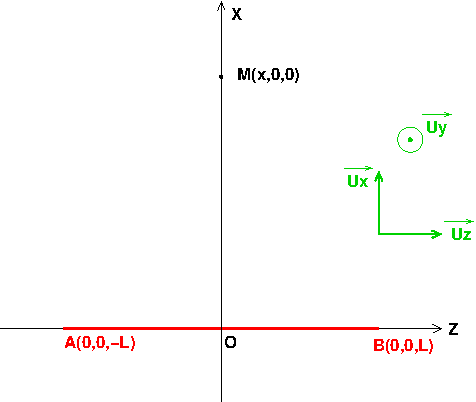
Comme sur le schéma que je te fournis, tu peux noter 2L la longueur de la tige chargée. Les plans (M,X,Z) et (M,X,Y) sont plans de symétrie pour la distribution de charges. Le vecteur champ en M doit appartenir à ces deux plans et donc être colinéaire à (O,X). Ce n'est pas ce que tu obtiens. Je me demande si tu as bien compris la notion de gradient. De façon générale, le gradient doit faire intervenir uniquement les dérivées par rapport aux coordonnées de position du point M où on étudie les propriétés du champ. Dans ce cas particulier :
De façon plus générale, les expressions de V et ne dépendent que des caractéristiques de la source (
et L et de la coordonnée de position x du point M.
Annuler
connectez vous