Niveau maths spé

electrostatique

Posté par
hiimgosu 03-10-17 à 21:46

Bonsoir , je voudrai avoir une piste pour cet exercice car je ne sais par ou le commencer :s
On considère un volume de plasma compris entre deux plans perpendiculaire a Ox et distants de h. On désigne no la densité particulaire à l'équilibre des électrons et des ions.
On suppose que les ions fixes et les électrons ne se deplaçant que selon Ox. On perturbe la distribution d'équilibre en déplaçant tous les électrons d'une distance x petite devant h.
1) La distribution de charge dans le plasma est assimilable quand x <> 0 , a deux plans portant des densité surfacique de charges uniformes D et -D . Déterminer D et en déduire l'expression de la force qui agit sur un électron par suite de perturbation.

Posté par re : electrostatique 03-10-17 à 22:24

Hello

Pour commencer tu peux te représenter 3 régions dans le volume de plasma

une première région "proche" (ie entre 0 et x) du premier plan où il y plus d'électrons: quelle étendue? quelle densité de charge?

une seconde région située à plus de x du premier plan: qui demeure électriquement neutre

une troisième proche du second plan (ie entre h-x et h) où il y un "excès" d'électrons.

si tu assimile la 1ere et la 3eme région des des plans (x petit devant h) tu peux alors considérer leurs densités de charges comme des densités surfaciques. Non?

Posté par re : electrostatique 03-10-17 à 22:26

$une première région$

Désolé j'ai cliqué sur poster plutôt que apercu. Il fallait lire

une première région "proche" (ie entre 0 et x) du premier plan où il n'y plus d'électrons: quelle densité de charge dans ce volume?

Posté par re : electrostatique 12-10-17 à 10:47

Pour ne pas laisser ce sujet en plan:

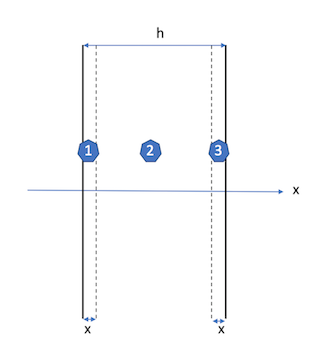
Dans la région (1) du schéma ci dessous:

La charge contenue dans un volume   $dV = xdydz$    est     $dq = +n_0edV = +n_0exdydz$

Si l'on confond cette charge élémentaire avec une charge surfacique sur la surface   $dxdy$ , on obtient une densité surfacique:     $D_+ = +n_0ex$ au voisinage du premier plan

De la même manière , au voisinage du 2nd plan, on a une densité surfacique   $D_- = - n_0ex$

En se souvenant de l'expression du champ électrique créé par un plan et en appliquant le Théorème de superposition:

Dans la région (2) il règne un champ uniforme   $\vec{E} = \frac{D}{\epsilon_0}.\vec{i}$

La force qui s'exerce sur un électron a donc pour valeur algébrique:

$F = -eE = -\frac{e^2n_0x}{\epsilon_0}$

Pour répondre à la question qui n'est pas posée.
En écrivant la RFD pour un électron de la région (2)

$m_e\ddot{x} +  \frac{e^2n_0}{\epsilon_0}x = 0$

Le électrons vont osciller à une pulsation proportionnelle à $\sqrt{n_0}$