Niveau licence

electrostatique

Posté par
ferenc 05-01-14 à 16:00

Bonjour.
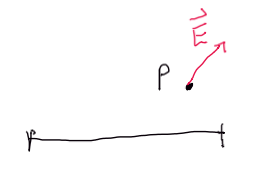
Considérons un fil de longueur $L$ de densité de charge $\lambda$ . Le champs électrique $\bold{E}$ au point $P$ serait plutôt de cette forme là, non ? (voir figure).

En d'autre terme, il est difficile d'utiliser le théorème de Gauss pour calculer les champs électrique des points qui sont situé à une même distance du fil, car on ne peut pas utiliser un élément de symétrie pour sortir $\bold{E}$ . En d'autre terme, si je prenais le cylindre de rayon $R$ et de longueur $L$ , je ne pourrais pas faire
$\int_{Cylindre}\bold{E}\cdot d\bold{S}=E 2\pi R^2L=\frac{\lambda L}{\varepsilon_0}$ et conclure que $E=\frac{\lambda L}{2\pi R^2 L}$ . Est-ce correct ou bien je me plante complètement ? Si le fil est de langueur infini pas de problème car le champs électrique est uniquement radial. Mais si le fil n'est pas de longueur infini, on est d'accord que ce n'est pas possible. Je me trompe ?

merci,

electrostatique

Posté par re : electrostatique 05-01-14 à 16:08

Bonjour.
Tu ne te trompes pas (mais il n'y a pas de R², seulement un R).
Mais il arrive quand même que l'on néglige les effets de bords, et donc on calcule le champ E avec le théorème de Gauss avec un fil de longueur finie (mais donc en toute rigueur c'est faux).

Posté par re : electrostatique 05-01-14 à 16:22

merci William (en effet pour le $R^2$ ^^). Donc viens du coup une autre question
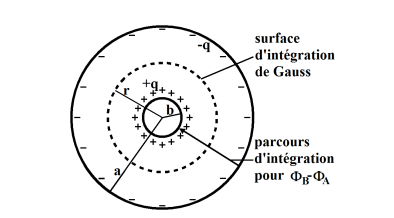
On considère un condensateur cylindrique formé de deux cylindre coaxiaux de longueur $L$ . Par symétrie, le champs $E$ est dans la direction radiale. Ainsi, $\int_S \bold{E}\cdot d\bold{S}=E2\pi rL$ ... on est bien d'accord que c'est faux puisque $E$ n'est pas constant sur $S$ (puisque les cylindre sont de longueurs fini). Peut-être avons nous négligé les effet de bord (mais j'en ai jamais entendu parlé au préalable, c'est pour ça que je ne comprend pas trop).

(En fait quand néglige les effet au bord, on suppose que les cylindres sont de longueurs infinies ??)

merci

electrostatique

Posté par re : electrostatique 05-01-14 à 16:29

On est bien d'accord, c'est faux.

En fait, lorsque l'on se situe vers le milieu du cylindre, et pas trop loin de lui, alors on perçoit presque la même chose que si le cylindre était infini. Et plus on s'approche du bord du cylindre, plus cette approximation est fausse.
Négliger les effets de bords signifie donc qu'on ne prend pas en compte cette erreur lorsqu'on s'approche du bord, et donc on calcule impunément avec le théorème de Gauss.

Cette tendance à négliger les effets de bord est motivée par deux choses :
D'une part, le calcul exact est compliqué même pour des géométries simples comme le fil ou le cylindre.
D'autre part, un cylindre infini ça n'existe pas, donc si on ne faisait jamais cette approximation alors le théorème de Gauss ne serait bon qu'à être jeté à la poubelle puisqu'on ne pourrait jamais s'en servir