Inscription / Connexion Nouveau Sujet
Electronique : filtre passe-bande ( erreur de montage )
Bonjour à tous, je suis en L2 Physique Chimie et je viens d'avoir TP d'électronique. Nous avons étudié les filtres passe-haut , passe-bas et passe bande. Sauf que pour le circuit passe-bande ci-dessous le circuit donné ne pourra jamais marcher - nous a dit le prof - car il y a une erreur dans le sens de montage ( il a fait le montage sur un binôme et a en gros sous entendu qu'il fallait inverser les montages RC et CR ). Voici le montage en question :
( C1 et C2 sont des condensateurs et R1 et R2 des résistances )
___R1_________C2____
| | |
| | |
Ve C1 (Vs)<-R2
| | |
|_______|____________|
Désolée pour le montage très mal fait : -Ve c'est le GBF réglé sur Fréquence:1kHz, Amplitude:10V et Vs est la tension aux bornes de R2 que l'on visualise sur l'oscilloscope en même temps que la tension d'entrée Ve.
Il nous a fait comprendre qu'avec ce montage et l'ordre des composants, on ne pourrait pas avoir de filtre passe bande. Pourquoi ?
Sottise.
Le filtre, tel quel, est bien un filtre passe bande.
La première cellule (R1C1) constitue un passe bas.
La seconde cellule (R2C2) constitue un passe haut.
L'ensemble des 2 cellules constitue bien un filtre passe bande.
Sans devoir faire des calculs pour le montrer, c'est évident.
Mais si on ne le "sent" pas, on peut calculer :
-----
Montrons-le :
Pas le courage de faire des calculs en littéral, je les faits avec des données numériques.
R1 = R2 = 1000 ohms
C1 = C2 = 10^-7 F
R2 serie C2 : Z2 = 1000 + 1/(jw.10^-7) = (1 + j.10^-4.w)/(j.10^-7.w)
C1 // Z2 : Z1 = [(1 + j.10^-4.w)/(j.10^-7.w * j.10^-7.w)]/ [(1 + j.10^-4.w)/(j.10^-7.w) + 1/(j.10^-7.w)]
Z1 = [(1 + j.10^-4.w)/(j.10^-7.w)]/(2 + j.10^-4.w)
Z1 = (1 + j.10^-4.w)/[(2 + j.10^-4.w).j.10^-7.w]
Ve/(R1 + Z1) = VC1/Z1
VC1 = Ve.Z1/(R1+Z1)
Z1/(R1+Z1) = [(1 + j.10^-4.w)/((2 + j.10^-4.w).j.10^-7.w)]/[R1 + (1 + j.10^-4.w)/((2 + j.10^-4.w).j.10^-7.w)]
Z1/(R1+Z1) = (1 + j.10^-4.w)/[1000.((2 + j.10^-4.w).j.10^-7.w) + (1 + j.10^-4.w)]
Z1/(R1+Z1) = (1 + j.10^-4.w)/[1000.((2 + j.10^-4.w).j.10^-7.w) + (1 + j.10^-4.w)]
Z1/(R1+Z1) = (1 + j.10^-4.w)/(2000 + j.10^-1.w).j.10^-7.w + 1 + j.10^-4.w)
Z1/(R1+Z1) = (1 + j.10^-4.w)/(2000 j.10^-7.w - 10^-8.w² + 1 + j.10^-4.w)
Z1/(R1+Z1) = (1 + j.10^-4.w)/(1 - 10^-8.w² + 3.10^-4.w.j)
VC1 = Ve.(1 + j.10^-4.w)/(1 - 10^-8.w² + 3.10^-4.w.j)
---
Vc1/(R2 + 1/(jwC2)) = Vs/R2
Vs = Vc1 * jwR2C2/(1 + jwR2C2)
Vs = Vc1 * jw.10^-4/(1 + jw.10^-4)
---
Vs = Ve.(1 + j.10^-4.w)/(1 - 10^-8.w² + 3.10^-4.w.j) * jw.10^-4/(1 + jw.10^-4)
Vs = Ve.jw.10^-4/(1 - 10^-8.w² + 3.10^-4.w.j)
---
|Vs/Ve| = 10^-4.w/[V((1 - 10^-8.w²)² + (3.10^-4.w)²)]
Vs/Ve = jw.10^-4/(1 - 10^-8.w² + 3.10^-4.w.j)
Vs/Ve = 10^-4/(-j(1 - 10^-8.w²)/w + 3.10^-4)
Vs/Ve = (1/3)/(1 + j.(10^-8.w² - 1)/(3.10^-4.w))
Vs/Ve = (1/3)/(1 + j.(3,333.10^-5.w - 3333/w))
Vs/Ve = (1/3)/(1 + j * (1/3)*(w/10^4 - 10^4/w))
A comparer avec Vs/Ve = Ho/(1 + j * Q*(w/wo - wo/w))
(Qui est la fonction de transfert d'un filtre passe-bande du second ordre, voir ici : 
)
Filtre passe bande avec les caractérisriques suivantes : Ho = 1/3 ; wo = 10^4 rad/s et Q = 1/3
-----
On peut inverser les 2 cellules ... on aura aussi un filtre passe bande, mais je ne refais pas les calculs pour montrer une 2eme fois l'évidence.
N'empêche, il n'y a aucune erreur de schéma, tel quel, on a bien un filtre passe-bande.
Sauf distraction. 
Je viens de demander à mon prof d'électronique , voici sa réponse :
" il faut que la fréquence du passe-haut 1/2piR2C2 soit plus petite que la fréquence de coupure du passe-bas 1/2piR1C1 dans votre schéma, sinon, rien ne passe : quand pour observer la courbe d'un passe-bande, les basses-fréquences ressemblent à un passe-haut et les hautes fréquences à un passe-bas.
Ici R2C2 doit être plus grand que R1C1... il faut donc bien choisir les composants. "
Je comprends pas totalement pourquoi si la fréquence de R1C1 est plus grande que R2C2 rien ne passe ?
On avait dans le TP des valeurs telles que :
C1= 1 nF
C2= 10 nF
R1 = 100 KOhms
R2= 1kOhms
du coup la fréquence de R1C1 ( filtre passe bas ) est de 1591,15 Hz et la fréquence de R2C2 ( filtre passe haut ) est de 15915,5 Hz . Donc comme il le dit rien ne passe car la fréquence de R2C2 est supérieur à celle de R1C1 . Mais je ne comprends pas pourquoi ça ne passe pas dans ce cas là ?
Merci pour vos réponses 
Cela fait déjà longtemps que quand je vois des exercices posés au niveau "License", je suis pratiquement certains d'y trouver des bourdes...
Etudions le quadripole suivant :
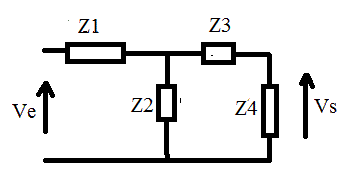
(Z3+Z4) // Z2 = Z2(Z3+Z4)/(Z2+Z3+Z4)
V(Z2)/[Z2(Z3+Z4)/(Z2+Z3+Z4)] = Ve/[Z1 + Z2(Z3+Z4)/(Z2+Z3+Z4)]
V(Z2)/[Z2(Z3+Z4)] = Ve/[Z1.(Z2+Z3+Z4) + Z2(Z3+Z4)]
Vz2 = Ve.Z2(Z3+Z4)/(Z1Z2+Z1Z3+Z1Z4+Z2Z3+Z2Z4)
-----
V(Z2)/(Z3+Z4) = Vs/Z4
Vs = V(Z2).Z4/(Z3+Z4)
Vs = Ve.Z2(Z3+Z4).Z4/[(Z3+Z4)(Z1Z2+Z1Z3+Z1Z4+Z2Z3+Z2Z4)]
Vs/Ve = Z2.Z4/(Z1Z2+Z1Z3+Z1Z4+Z2Z3+Z2Z4)
---------
1) Attribuons aux différentes impédances, les caractéristiques pour que le quadripole ci-dessus corresponde à celui dessiné.
Si Z1 = R1, Z2 = 1/(jwC1), Z3 = 1/(jwC2) et Z4 = R2, il vient : (donc cellules mises comme sur ton schéma du post initial)
Vs/Ve = (R2/(jwC1))/[R1/(jwC1) + R1/(jwC2) + R1R2 + 1/(j²w²C1C2) + R2/(jwC1)]
Vs/Ve = R2/[R1 + R1.C1/C2 + jwR1R2C1 + 1/(jwC2) + R2]
Vs/Ve = jwR2C2/(jwR1C2 + jw.R1.C1 + j²w²R1R2C1C2 + 1 + jwR2C2)
Vs/Ve = jwR2C2/[(1 - w²R1R2C1C2) + jw(R1C2 + R1.C1 + R2C2)]
-----
2) Attribuons aux différentes impédances, les caractéristiques pour que le quadripole du-dessus correponde à celui dessiné mais dans lequel on aurait croisé les 2 cellules.
Si Z1 = 1/(jwC2), Z2 = R2, Z3 = R1 et Z4 = 1/(jwC1) : (donc cellules croisées par rapport à ton schéma)
Vs/Ve = (R2/(jwC1))/(R2/(jwC2) + R1/(jwC2) + 1/(j²w²C1C2) + R1R2 + R2/(jwC1))
Vs/Ve = R2/(R2C1/C2 + R1.C1/C2 + 1/(jwC2) + jwR1R2C1 + R2)
Vs/Ve = jwR2C2/(jwR2C1 + jwR1.C1 + 1 + j²w²R1R2C1C2 + jwR2C2)
Vs/Ve = jwR2C2/[(1 - w²R1R2C1C2) + jw(R2C1 + R1.C1 + R2C2)]
-----
Et pan dans les dents.
On trouve la même fonction de transfert avec les cellules comme dans ton schéma ou bien avec les cellules croisées.
Je te laisse en tirer les conclusions, sur le fait que ce "schéma aurait un problème".
Mais le prof a toujours raison ... même quand il a tort.
Il faut évidemment choisir les bonnes valeurs de composants en fonction de la bande qu'on veut laisser "passer", mais croiser ou non les cellules revient du pareil au même.
Il faut évidemment penser (ce qu'on ne fait quasi jamais dans l'enseignement (à grand tort)) qu'un filtre non muni de sa "charge" n'a pas la même fonction de transfert qu'en utilisation dans les cas pratiques ... et donc avec une charge à la sortie du filtre... mais c'est une autre histoire.
Je vois à peu près ce que tu viens de me dire . Mais sachant que dans le TP on avait Z4 
Z2 . Y a -t-il un impact sur le filtre passe bande ? Je ne comprends toujours pas pourquoi le prof me dit " il faut que la fréquence du passe-haut 1/2piR2C2 soit plus petite que la fréquence de coupure du passe-bas 1/2piR1C1 dans votre schéma, sinon, rien ne passe " ? Serait-ce donc une erreur de sa part ?
En tout cas merci ça me permet de mieux comprendre le circuit avec tes explications
Avec les valeurs numériques du post du 27-11-13 à 14:52, on arrive à :
Vs/Ve = jwR2C2/[(1 - w²R1R2C1C2) + jw(R2C1 + R1.C1 + R2C2)]
Vs/Ve = jw.10^-5/((1 - 10^-9.w²) + jw.1,11.10^-4)
|Vs/Ve| = w.10^-5/[V((1 - 10^-9.w²)² + (w.1,11.10^-4)²)]
Centrée sur f = 5033 Hz, |Vs/Ve|max = 0,09
B(à-3dB) (de 1333 Hz à 19000 Hz)
-----
On voit donc, par |Vs/Ve|max = 0,09, que la sortie est de très faible amplitude ... même à la fréquence fo.
Mais cela donnerait la même chose en croisant les 2 cellules.
-----
La remarque sur le schéma est sans fondement, il n'empêche que, comme je l'ai déjà dit, les composants doivent être choisis judicieusement pour avoir ce qu'on veut.
A partir de Vs/Ve = jwR2C2/[(1 - w²R1R2C1C2) + jw(R1C2 + R1.C1 + R2C2)] de mon message précédent, il faut faire le petit effort pour mettre sous la forme : Vs/Ve = Ho/(1 + j * Q *(w/wo - wo/w)) classique pour discuter des caractéristiques du filtre.
Et choisir les composants pour approcher au mieux les Ho, Q et wo pour obtenir la réponse désirée.
... Mais pas croiser les cellules, c'est inutile. 
Je ne comprends toujours pas pourquoi le prof me dit " il faut que la fréquence du passe-haut 1/2piR2C2 soit plus petite que la fréquence de coupure du passe-bas 1/2piR1C1 dans votre schéma, sinon, rien ne passe " ?
En fort simplifié (et donc pas très rigoureux, mais pour faire comprendre)
Un filtre passe bande a une partie qui atténue les fréquences inférieures à une certaines valeur A et une autre qui atténue les fréquences supérieures à une certaine autre valeur B.
Si B > A, alors on atténue fortement toutes les fréquences, il ne reste presque rien à la sortie.
Il reste quand même un petit quelque chose à la fréquence fo ... mais ce n'est q'un tout petit quelque chose (qui dans l'exampple donné correspond à |Vs/Ve|max = 0,09 ... soit vraiment pas grand chose.
Ici, ce qui est au dessus de 1500 Hz est atténué par le partie passe-bas du filtre.
Ce qui est en dessous de 15000 Hz est atténué par la partie passe-haut du filtre.
Il n'y a donc pas de zone de fréquence qui ne subit pas l'atténuation d'au moins une des 2 parties du filtre... et donc la sorie est forcément "faible" à toute fréquence. Juste un peu moins faible (mais pas forte) près de fo.
Ah super merci je pense comprendre , sauf erreur de ma tête blonde :
Ici, ce qui est au dessus de 1500 Hz est atténué par le partie passe-bas du filtre.
Ce qui est en dessous de 15000 Hz est atténué par la partie passe-haut du filtre.
Il n'y a donc pas de zone de fréquence qui ne subit pas l'atténuation d'au moins une des 2 parties du filtre... et donc la sorie est forcément "faible" à toute fréquence. Juste un peu moins faible (mais pas forte) près de fo.
En gros ce filtre là atténue tout ce qui est entre 1500HZ et 15KHz , grêce aux deux parties du filtre ce qui fait qu'il ne reste pas grand chose qui peut passer si je comprends ?
Or si on avait une fréquence de coupure du filtre passe haut plus faible que celle du filtre passe-bas, si je prends des valeurs fictives comme 1500Hz pour le filtre passe bas ( donc tout ce qui est au dessus est enlevé ) et de par exemple 1000Hz pour le filtre passe haut ( donc tout ce qui est au dessous est enlevé ) ça marcherait ... ? En gros la bande passante serait entre 1000 et 1500 Hz ?
Bon j'ai à peu près compris le problème mais je ne pense pas que mon raisonnement dans le commentaire précédent soit bon .
|Vs/Ve| = w.10^-5/[V((1 - 10^-9.w²)² + (w.1,11.10^-4)²)] dans ce calcul là, w on le remplace par quelle valeur ?
w = 2Pi.f
f est la fréquence en Hz et w est appelée pulsation (en rad/s)
On ne remplace par w par une valeur.
Le but est de tracer le graphe de |V/Ve| en fonction de w (ou de f) ... pour visualiser le comportement du filtre aux différentes fréquences.
On présente souvent ce graphe avec une échelle logarithmique sur l'axe des abscisses représentant w (ou f) et souvent on met 20.log|V/Ve| en ordonnées. Ce n'est pas obligatoire mais c'est plus "parlant".
Voila alors ce que cela donne (pour le filtre en question).
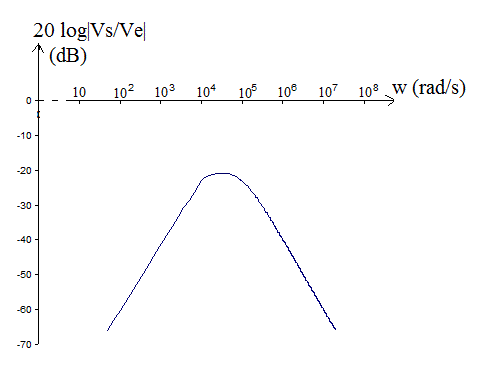
Attention que l'axe des abscisses est en graduations logarithmiques.
-----
C'est bien pour w = 31620 rad/s (soit pour f = 5033 Hz) (attention en mesurant ... éhcelle logarithmique) que le filtre atténue le moins fort ... Mais on a, à cette fréquence 20.log|Vs/Ve| = -21 dB(environ), donc |Vs/Ve| = 0,09 environ
Et on voit bien les 2 pentes à 20 dB/décade du filtre.
Le filtre est bien un "passe-bande" ... mais avec une atténuation forte même en fo.
Ahhh super merci beaucoup ! Je viens d'apprendre que j'ai 20/20 à ce TP car j'ai réexpliquer au prof tout ce que vous venez de me dire , du coup il a décidé de mettre un 20 ! Merci beaucoup pour toutes ces explications !
Annuler
connectez vous