Inscription / Connexion Nouveau Sujet
Électromagnétostatique
Bonjour à tous,
Je dois passer un examen en Électromagnétostatique la semaine prochaine et je galère sur un exo ou plutôt juste une question :
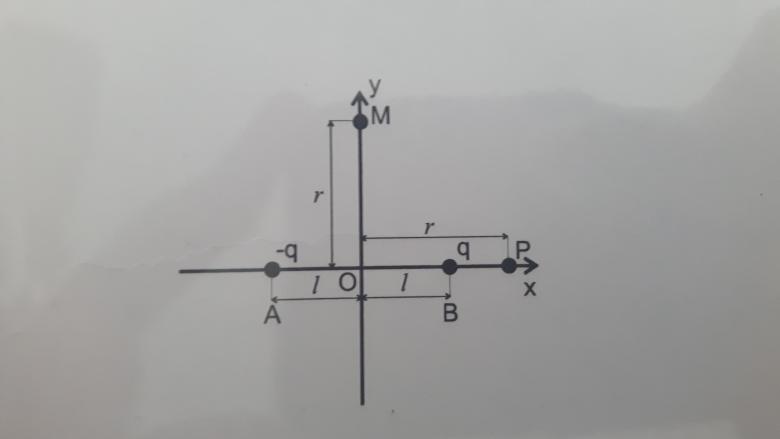
Déterminer le champ électrostatique E en un point P de l'axe Ox, comme indiqué sur le schéma.
La question est simple j'ai réussi à le faire au point M mais pour moi au point P le champ est nul...
Je n'arrive pas à représenter les champs EA et EB sur le schéma
J'ai un résultat déjà donné mais je veux le retrouver par moi même :
E = q/4
 0
0  ((4xl)/((x2-l2)2))
((4xl)/((x2-l2)2))
Merci d'avance pour votre réponse !
AR2
Bonjour
au point P le champ est nul
Non ! En P les deux vecteurs champs ont même direction, des sens opposés mais la norme du vecteur champ créé par qB est supérieure à la norme du vecteur champ créé par (-qA) .
Le vecteur champ résultant a la direction commune aux deux vecteurs précédents, le sens du vecteur de plus grande norme et pour norme : la différence des deux normes...
Je te laisse réfléchir et proposer une solution...
Merci de votre réponse !
J'ai réfléchi et ce qui me pose problème c'est d'exprimer les normes de EA et EB
Parce que si j'ai bien réfléchi :
E =  projections des EA et EB sur Ox
projections des EA et EB sur Ox
Je n'arrive pas écrire les projections...
Merci d'avance
AR2
En définissant un vecteur unitaire suivant l'axe (O,x), les vecteurs champ en P ont pour expressions :
Je te laisse terminer... Ce calcul me parait plus simple que celui du vecteur champ en M...
Bonjour vanoise,
Il faudrait que je m'y remette, mais j'ai un doute:
Avec ta réponse, que le point P soit placé à gauche de A, entre A et Bou à droite de B, les champs EA et EB restent dans le même sens...
Bonjour sanantonio312
les champs EA et EB restent dans le même sens...
EA et EB désignent les vecteurs champ créés au même point P par les charges situées respectivement en A et en B.
Une charge positive crée un champ de vecteur radial centrifuge, une charge négative crée en champ radial centripète... Pour t'en convaincre, imagine une charge d'essai ponctuelle positive qo placée en P. La charge négative placée en A exercerait sur elle une force attractive, la charge positive placée en B exercerait sur elle une force répulsive et comme :
Je te laisse conclure...
Les remarques et les équations écrites dans mon message du 18-05-18 à 20:42 sont valides pour un point P placé, conformément au schéma, à droite de B.
Une autre étude, non demandée ici apparemment, consisterait à étudier les variations du champ électrique résultant en fonction de x, l'abscisse de P...
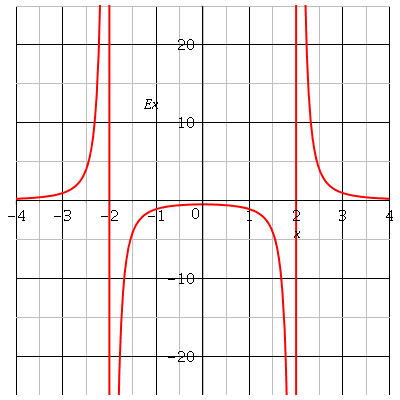
Pour compléter mon message précédent : voici la courbe représentant les variations en fonction de l'abscisse x de P de Ex : composante non nulle du vecteur champ résultant en P. J'ai choisi arbitrairement l=2 ; unités arbitraires pour les deux axes.
x<-l : EA et EB sont de sens opposés, le sens du vecteur somme est celui du vecteur de plus grande norme : EA, le sens positif.
-l<x<l : les deux vecteurs sont de même sens : le sens négatif.
x>l : EA et EB sont de sens opposés, le sens du vecteur somme est celui du vecteur de plus grande norme : EB, le sens positif.
Évidemment, la courbe présente des asymptotes verticales en x=-l et x=l.