Inscription / Connexion Nouveau Sujet
Electromagnétisme : faisceau de particules
Bonjour
un classique:
j'ai un faisceau (cylindre de rayon et d'axe
) de particule homogène de particules de charge individuelle
qui se déplace à la vitesse
la densité particulaire est
j'ai déterminé et
pour un point (
) à l'extérieur du cylindre j'ai déterminé
et
avec
la hauteur du cylindre de la surface de Gauss
ma question porte sur la suite:
j'ai un nouveau référentiel en translation à la vitesse
par rapport à
j'ai "établit" que et
maintenant comment déterminer les champs et
dans
***Edit gbm ;
- titre changé pour plus de clarté ;
- niveau mis en accord avec ton profil, merci de faire de même la prochaine fois***
Bonsoir,
Je suis d'accord avec ton expression du vecteur champ d'induction magnétique mais tu as commis une erreur sur le vecteur champ électrique : sa norme doit être proportionnelle à n et ne doit pas dépendre de h puisque le cylindre est supposé infiniment long (tu ne l'as pas dit mais ton expression de B n'est valide que dans ce cas...)
Pour la suite, tu pourras t'inspirer du paragraphe A du chapitre 4 page 163 de la référence : ![]()
j?appelle
la hauteur de ma surface de Gauss
et après c'est la que je ne sais plus comment procédé pour obtenir pour appliquer le théorème de Gauss
***Image recadrée***
Bonsoir,
l'expression du flux que tu viens d'obtenir, s'écrit, selon le théorème de Gauss :
La charge située dans le volume délimitée par la surface de Gauss est celle contenue dans le cylindre de rayon a et de hauteur h :
Je te laisse finir...
d'accord c'est ce qu'il me semblait
je ne savais pas bien quelle surface il fallait choisir, il s'agit du cylindre chargé à l'intérieur du grand cylindre
merci
Pour la suite, tu pourras t'inspirer du paragraphe A du chapitre 4 page 163 de la référence :
ces pages là ne sont pas consultables sans avoir acheté le bouquin du coup donne moi simplement la façon de faire pour déterminer les champs
sachant que je pense devoir trouver des résultats qui ne sont pas en accord avec les changement de référentiel dans la mécanique newtonienne à savoir:
mais conforme à ceux d'Einstein
je n'ai obtenu ni l'un ni l'autre je ne sais pas comment procédé ...
ce n'est pas les techniques normales à savoir théoreme de Gauss et d'Ampere ?
A ma connaissance, il y a deux méthodes :
en théorie classique : utiliser la méthode décrite dans le Bréal cité en référence : imaginer une particule de charge qo se déplaçant à la vitesse vo par rapport à la source. Ecrire que cette particule est soumise à la même force électromagnétique de Lorentz dans le repère R et dans le repère R*.
la théorie relativiste raisonne sur l'écriture des équations de Maxwell dans les deux repères. Cela n'est certainement pas à ton programme.
P.S. : force de Lorentz généralisée :
Si, justement les équation de Maxwell et le changement de référentiel par conservation de la force de Lorentz est au programme et donnent
(1)
mais on sait aussi que pour des vitesses proches de la lumière ce modèle ne convient plus et on utilise :
(2)
ces deux résultats me sont donnés pour répondre à la question. Mais je me demande simplement si il y a une manière "à la main" de déterminer ces deux champs sans utiliser de formule pour montrer si l'on se trouve dans l'un des cas (1) ou (2)
ce qui n'est pas au programme par contre c'est la loi de Biot et Savart, tout l'objet de l'exercice que je fais est de comprendre le fonctionnement de cette loi sans vraiment l'utiliser..
ok merci,
j'ai encore un soucis:
J'ai spire circulaire dont l'axe contient un point tel que
, on me dit qu'elle peut être vu comme un dipôle.
** image supprimée **
Je dois vérifer que le champ en est cohérent avec le modèle du dipôle à savoir
avec
J'ai dit que les plans et
étaient des plans d'antisymétrie pour
donc de
colinéaire à
mais pour le reste je ne vois pas
les invariances par rotations (et translation) le long de (autour de)
donnent comme
on a :
je n'obtiens donc pas le dipôle
Revois comment sont définis r,  et les vecteurs unitaires er et e
et les vecteurs unitaires er et e dans le cours conduisant à l'expression de B du dipôle.
dans le cours conduisant à l'expression de B du dipôle.
Il est probable que  désigne l'angle entre (Oz) et (OM) de sorte que le cas particulier où M est sur l'axe (Oz) corresponde au cas
désigne l'angle entre (Oz) et (OM) de sorte que le cas particulier où M est sur l'axe (Oz) corresponde au cas  =0 et er confondu avec ez.
=0 et er confondu avec ez.
tu as raison, pour établir cette expression on a fait l'analogie avec ce qui avait été démontré pour le dipole electrostatique et où on c'était placé dans les coordonnées sphériques.
mais dans notre cas les coordonnées sphériques ne sont pas recommandées car on est sur un axe
ma question est donc comment établir la forme du champ magnétique d'un dipôle dans les coordonnées cylindriques pour pouvoir comparer.
ma question est donc comment établir la forme du champ magnétique d'un dipôle dans les coordonnées cylindriques pour pouvoir comparer.
Je saurais répondre très facilement à ta question en utilisant la loi de Biot et Savart. Sinon...?
J'avoue ne pas très bien "sentir" l'esprit de ce nouveau programme et surtout le but de cet exercice : supprimer la loi de Biot et Savart et privilégier le théorème d'Ampère, c'est exactement comme supprimer en électrostatique la loi de Coulomb et tout vouloir démontrer à partir du théorème de Gauss...
mon prof a exactement la même mentalité que toi à ce sujet
mais bref nous on est étudiant on subit on n'a pas notre mot à dire et il faut réussir le concours avec le programme qu'on nous donne BREF
la loi de Biot et Savart me donne : dans le cas où ,
mais ce n'est pas la question cette loi de Biot et Savart me donne le résultat du cercle chargé, moi ce que je cherche à démontrer c'est que cette expression du cercle chargé correspond à un dipôle ...
Voici je crois le "maillon manquant" à ton raisonnement.
Reprends ta définition du vecteur moment magnétique d'un circuit filiforme fermé .
Remarque ensuite que le produit vectoriel :
représente l'aire du circuit balayée par le vecteur OM lorsque M se déplace de dl dans le sens du courant le long de la spire (voir cours de math).
Dans le cas simple d'un circuit filiforme fermé et plan, le vecteur moment magnétique du circuit est simplement :
où le vecteur surface est perpendiculaire au plan de la spire, orienté en fonction du sens du courant selon la règle du tire-bouchon de Maxwell, sa norme étant l'aire de la surface délimitée par la spire.
Dans le cas d'une spire de rayon R orientée conformément à ton schéma :
Tu est sûrement capable de terminer...
L'exportation de mon schéma au format jpeg décale légèrement la spire par rapport au reste du schéma ; cela ne devrait pas trop te gêner...
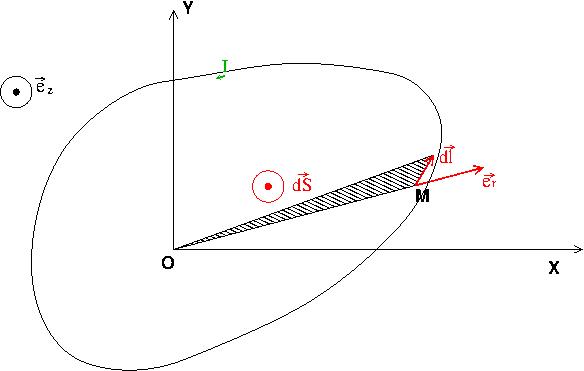
L'exportation de mon schéma au format jpeg décale légèrement la spire par rapport au reste du schéma ; cela ne devrait pas trop te gêner...
et dire que ca aurait pu etre parfait



