L'espace compris entre deux plans de cote - e/2 et e/2 est rempli de dîpole microscopique régulièrement répartis. Un volume mesoscopique élémentaire d possède un moment dipolaire dp = p*d.

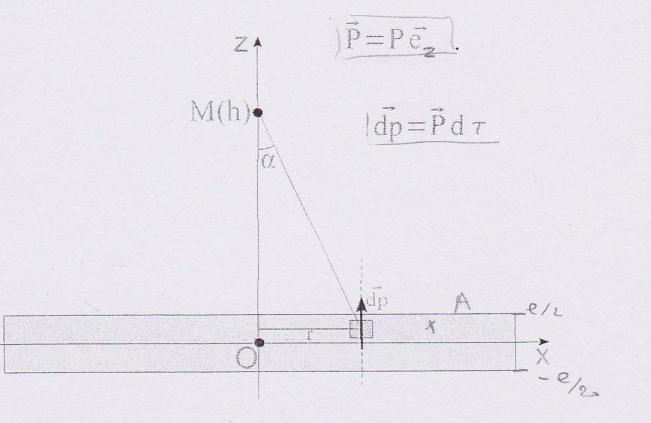
Le vecteur p, densité volumique de moment dipolaire encore appelé vecteur polarisation est ici uniforme : p = p*e_z

1°) Un point A situé entre les plans de cote -e/2 et e/2 est repéré par ses coordonnées cylindrique (r,,z). Exprimer le potentiel dV crée par les dipoles situés dans l'élément de volume d situé au voisinage de A, en un point M situé sur l'axe (Oz) à la cote h. On pourra utiliser l'angle

Regarder la figure pour plus de clarté

Réponse :

dV(M) = grav V . dOM = - E.dOM

Or E = ( dp * OM ) / (4₀*OM²)

et dOM = h . e_z

En injectant les expressions que j'ai écrite dans l'énoncé, je trouve -( p*d) / (4₀*h²)

Mais déjà, c'est pas homogène donc mal barré ....

Je peux pas avancer sans cette question donc un peu d'aide serait le bienvenu s'il vous plait.

Je donne la suite de l'exo si je bloque...


2°) Déduire le potentiel et le champ électrique en M lorsque h<-e/2, -e/2 < h < e/2, h>e/2

3°) Mq cette distribution de dipoles est équivalente à une distribution de charges que l'on précisera.