Inscription / Connexion Nouveau Sujet
Électromagnétisme : champ créé par un fil
Bonsoir à tous et chacun.
J'aimerais bien que vous jetez un coup d'œil sur ma proposition de réponse pour cet exercice.
Exercice :
Soit un fil de longueur L portant une densité de charge 
1- Trouver l'expression du champ électrostatique en M situé à une distance x sur la médiatrice du fil.
2- Que deviennent ces expressions quand le fil est infini?
3- Composer au résultat obtenu en utilisant le théorème de Gauss.
Ma proposition de réponse :
1-
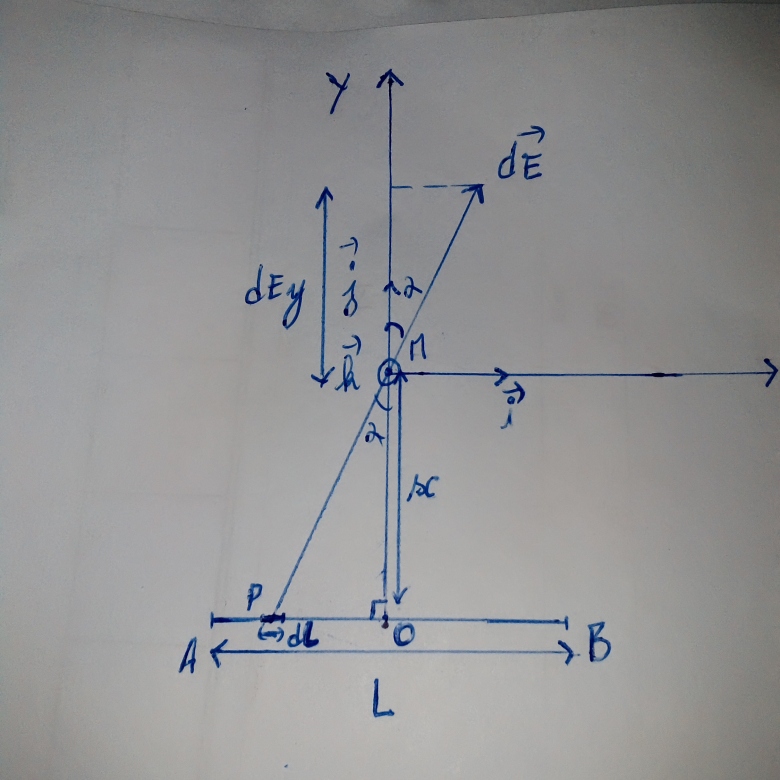
Soit PO= L
L
Plans de symétries: (M, ,
, ); (M,
); (M, ,
, )
)
Alors le champ  ) est suivant l'axe (M,
) est suivant l'axe (M, )
)
d o)(
o)(
<br />PMy=OM=x
<br />PM=(x²+[smb]beta.gif) ²L²)½ avec PM=(PO²+OM²)½ où PO=
²L²)½ avec PM=(PO²+OM²)½ où PO= L
L
dEy=(( dLx)÷(4π
dLx)÷(4π o(x²+
o(x²+ ²L²)^³(½)
²L²)^³(½)
tan =(
=( L)÷x
L)÷x  dL=(x÷
dL=(x÷ )(1+tan²
)(1+tan² )d
)d
alors dEy=( (x²÷
(x²÷ )(1+tan²
)(1+tan² )d
)d )/(4π
)/(4π o(x²+
o(x²+ ²L²)^³(½))
²L²)^³(½))
Ey=( ÷4π
÷4π o
o x)
x) cos
cos d
d (pris entre -
(pris entre - et
et  )
)
Ey=( (2sin
(2sin )÷(4π
)÷(4π o
o x
x
Or Sin =(
=( L)/(x²+
L)/(x²+ ²L²)^½)
²L²)^½)
Ey=( L)/(2π
L)/(2π ox(x²+
ox(x²+ ²L²)^½)^½).
²L²)^½)^½).
2-
Quand le fil est infini:
- soit L

Dans ce cas Ey=0
-soit  variant de -π/2 à π/2.
variant de -π/2 à π/2.
Dans ce cas Ey= /(2π
/(2π
 ox)
ox)
Ses différents résultats m'inquiète et je me demande là où j'ai fais erreur. Votre aide me sera précieuse.
3- Pour cette question, je n'arrive pas à cerner la tâche à accomplir ( je ne comprend pas la question).
Au début j'avais mis : vecteur dE=( dL)/(4π
dL)/(4π o)(vecteur PM÷PM³)
o)(vecteur PM÷PM³)
Pour la figure quand j'appuie sur "choisir un fichier " ça ne répond ( aucune réaction). C'est pourquoi je n'ai pas encore envoyé la figure.
Bonjour
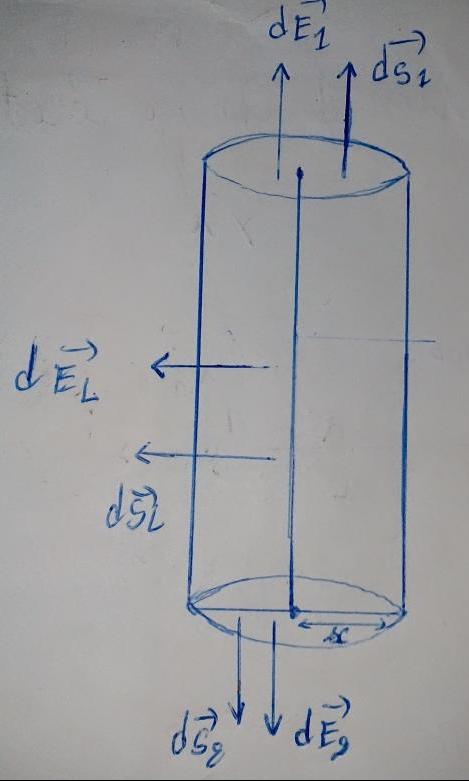
Pour le fil de longueur infinie, la source possède suffisamment de symétries et d'invariances pour que tu puisses appliquer le théorème de Gausse à un cylindre d'axe confondu avec le fil, de rayon r=x et de hauteur h quelconque (h disparait en fait du calcul ensuite par simplifications).
Sinon, pour le fil de longueur finie, poser, si je comprends bien : OP= .L dans l'expression du vecteur champ élémentaire, conduit ensuite à intégrer entre
.L dans l'expression du vecteur champ élémentaire, conduit ensuite à intégrer entre  =-0,5 et
=-0,5 et  =0,5.
=0,5.
 ne doit pas apparaître dans le résultat.
ne doit pas apparaître dans le résultat.
Si je comprend bien, il faut que j'intègre le résultat que j'ai obtenir en 1 en considérant que  varie entre(-0.5 et 0.5). Or normalement pour intégrer il faut qu'il ait le différentiel du variable( soit d
varie entre(-0.5 et 0.5). Or normalement pour intégrer il faut qu'il ait le différentiel du variable( soit d dans ce cas; ce qui ne trouve ni dans l'expression de dE, ni dans celle de E) dans l'expression à intégrer, afin que l'on ait(
dans ce cas; ce qui ne trouve ni dans l'expression de dE, ni dans celle de E) dans l'expression à intégrer, afin que l'on ait( kd
kd ) et non (
) et non ( k) avec k l'expression à intégrer. Comment ferais-je apparaître d
k) avec k l'expression à intégrer. Comment ferais-je apparaître d dans l'expression pour pouvoir intégrer par rapport à
dans l'expression pour pouvoir intégrer par rapport à  ? Ou mettrai-je tout simplement (
? Ou mettrai-je tout simplement ( Ed
Ed ?
?
De plus je n'arrive pas assimilé le fait que  doit varier de -0.5 à 0.5.
doit varier de -0.5 à 0.5.
Ensuite pouvait-on tendre L vers infini ou prendre  entre -π÷2 et π÷2 , pour le cas d'un fil infini ? Si oui, pourquoi j'ai trouvé des réponses différentes pour ces deux cas(voir ma proposition de réponse : question 2)
entre -π÷2 et π÷2 , pour le cas d'un fil infini ? Si oui, pourquoi j'ai trouvé des réponses différentes pour ces deux cas(voir ma proposition de réponse : question 2)
Enfin une traduction de la question 3, est-ce : Reprenez les questions précédentes en utilisant le théorème de Gauss ? Si oui je pense que l'utilisation du cylindre que vous avez énoncé pour le fil infini (si je comprend la question 2 pour l'utilisation du théorème de Gauss) est bonne: Quand je l'ai fais le flux au niveau des deux surfaces de bases est nulle et celui de la face latérale donne 2πxhE et après l'application du théorème de Gauss, je trouve E=( )/(2π
)/(2π ox)(h est bien disparu par simplication comme vous l'aviez énoncé).
ox)(h est bien disparu par simplication comme vous l'aviez énoncé).
Et alors comment utiliser le théorème de Gauss pour le cas d'un fil fini de longueur L(première question)?
Si vous me le permettez :
En éffet mon message précédent est rempli de petites erreurs que j'ai dû corrigé. Excusez-moi beaucoup.
Si je comprend bien, il faut que j'intègre le résultat que j'ai obtenir en 1 en considérant que  varie entre(-0.5 et 0.5). Or normalement pour intégrer il faut qu'il ait le différentiel du variable( soit d
varie entre(-0.5 et 0.5). Or normalement pour intégrer il faut qu'il ait le différentiel du variable( soit d dans notre cas; ce qui ne se trouve ni dans l'expression de dE, ni dans celle de E) dans l'expression à intégrer, afin que l'on ait(
dans notre cas; ce qui ne se trouve ni dans l'expression de dE, ni dans celle de E) dans l'expression à intégrer, afin que l'on ait( kd
kd ) et non (
) et non ( k) avec k l'expression à intégrer. Comment ferais-je apparaître d
k) avec k l'expression à intégrer. Comment ferais-je apparaître d dans l'expression pour pouvoir intégrer par rapport à
dans l'expression pour pouvoir intégrer par rapport à  ? Ou mettrai-je tout simplement (
? Ou mettrai-je tout simplement ( Ed
Ed )?
)?
De plus je n'arrive pas à assimiler le fait que  doit varier de -0.5 à 0.5.
doit varier de -0.5 à 0.5.
Ensuite pouvait-on tendre L vers infini ou prendre  entre -π÷2 et π÷2 , pour le cas d'un fil infini ? Si oui, pourquoi j'ai trouvé des réponses différentes pour ces deux cas(voir ma proposition de réponse : question 2)
entre -π÷2 et π÷2 , pour le cas d'un fil infini ? Si oui, pourquoi j'ai trouvé des réponses différentes pour ces deux cas(voir ma proposition de réponse : question 2)
Enfin une traduction de la question 3, est-ce : Reprenez les questions précédentes en utilisant le théorème de Gauss ? Si oui je pense que l'utilisation du cylindre que vous avez énoncé pour le fil infini (si je reprend la question 2 pour l'utilisation du théorème de Gauss) est bonne: Quand je l'ai fais le flux au niveau des deux surfaces de bases est nulle et celui de la face latérale donne 2πxhE et après l'application du théorème de Gauss, je trouve E=( )/(2π
)/(2π ox)(h est bien disparu par simplication comme vous l'aviez énoncé).
ox)(h est bien disparu par simplication comme vous l'aviez énoncé).
Et alors comment utiliser le théorème de Gauss pour le cas d'un fil fini de longueur L(si je reprend la première question en utilisant le théorème de Gauss comme demandé à la troisième questions)?
En posant ,
varie entre -L/2 et L/2 ;
 varie donc entre -0,5 et 0,5. Cependant, le calcul intégral qui résulte du choix de la variable
varie donc entre -0,5 et 0,5. Cependant, le calcul intégral qui résulte du choix de la variable  conduit à un calcul d'intégrale pas tout à fait évident. Il est beaucoup plus simple de choisir comme variable d'intégration l'angle
conduit à un calcul d'intégrale pas tout à fait évident. Il est beaucoup plus simple de choisir comme variable d'intégration l'angle  . Ainsi :
. Ainsi :
La longueur élémentaire centrée en P devrait être notée d(OP) ou dP mais pas dL ; ce qui t'as induit en erreur. En différentiant l'expression de , on obtiendrait avec ton choix de variable :
Avec mon choix :
Il n'est pas non plus astucieux d'avoir noté x la distance OM tout en notant dEy la composante du vecteur champ colinéaire à OM mais après tout. Bref : cette composante peut s'écrire :
Plutôt facile comme calcul intégral ! Je te laisse terminer et vérifier que la simplification correspondant à L>>x, c'est à dire à  variant entre -
variant entre - /2 et
/2 et  /2, conduit bien à la même expression du vecteur champ que celle obtenue à partir du théorème de Gauss.
/2, conduit bien à la même expression du vecteur champ que celle obtenue à partir du théorème de Gauss.
Lorsque j'applique ce que vous m'avez conseillé, l'expression de Ey trouvé correspond exactement à celle trouvé par le théorème de Gauss.
Pourtant j'ai toujours des préoccupations concernant l'une des étapes qui a conduit à tel résultat :
En éffet, pour ce que je pense savoir (la compréhension que j'ai du cour)
dEy=( dLPMy)(4π
dLPMy)(4π oPM³)
oPM³)
Avec L, la longueur du fil chargé. Et donc dL ne représente que la longueur infinitésimale du fil chargé.
Ma première préoccupation est celle-ci: pourquoi dOP doit être dans l'expression au détriment de dL?(ça m'inquiète beaucoup.)
Ma seconde préoccupation est celle-ci:
Comment trouver le champ du fil fini de lire L en utilisant le théorème de Gauss ?(Question 3 de l'exercice qui demande à ce qu'on reprenne les questions 1 et en utilisant le théorème de Gauss si j'ai bien compris )
Ma dernière préoccupation est:
Est-ce que le choix de la variation de  (variant de-π/2 à ÷/2, -
(variant de-π/2 à ÷/2, - à
à  ) dépend du repère choisi ? En éffet moi
) dépend du repère choisi ? En éffet moi
j'utilise ça dans ce cas car: comme le point M origine de mon repère, se trouve sur la médiatrice du fil, les extrémités du fil prennent respectivement les valeurs -L/2 et L/2( selon moi ça dépend du repère.)
La lettre « d » devant le symbole d'une grandeur (ici « L ») correspond à une variation élémentaire de celle-ci, assimilable mathématiquement à une différentielle. Or, dans ce problème, L est une constante. C'est qui varie entre -L/2 et L/2. Cela dit, il s'agit juste d'un problème de notation car l'expression de dEy que tu fournis, montre que tu as compris l'essentiel. Plusieurs choix sont possibles comme variable de position du point P : la valeur de
, la valeur de
 , la valeur de l'angle
, la valeur de l'angle  . Ce qu'il faut bien comprendre : si tu introduis
. Ce qu'il faut bien comprendre : si tu introduis  comme variable de position, il ne faut pas considérer
comme variable de position, il ne faut pas considérer  comme une constante dans le calcul intégral. Il se trouve que le calcul intégral est beaucoup plus simple en faisant intervenir comme variable d'intégration l'angle
comme une constante dans le calcul intégral. Il se trouve que le calcul intégral est beaucoup plus simple en faisant intervenir comme variable d'intégration l'angle  comme je te l'ai montré dans mon message précédent.
comme je te l'ai montré dans mon message précédent.
Comment trouver le champ du fil fini de lire L en utilisant le théorème de Gauss ?
Le théorème de Gauss n'est pas applicable de façon simple dans le cas d'un fil de longueur finie. En effet, l'application simple du théorème suppose que la norme du vecteur champ ne dépend que de la distance au fil et est en tout point normal à la surface du cylindre de Gauss. Cela n'est vrai que pour le fil de longueur infinie.
Bonjour.
Si je comprend bien pour tous les exercices concernant un fil fini, c'est le point d'où le champ est créé(Dans notre cas ci: le point p) qui subit une variation. Et donc pour le repérage nous allons donc projeté l'origine ( M dans notre cas) du repère sur le fil ( Soit O ici) et là c'est ( dOP qui subira de déformation pour la construction du fil: soit une sommation de dOP.): Et là pour former le fil, P doit faire une variation consistant à quitter une extrémité du fil pour aller à l'autre extrémité. Les extrémités étant des point, peuvent être repérer( dans notre cas leur ordonné est nulle et on a respectivement -L/2 et L/2 pour chacune des extrémités). Et donc je P varie de -L/2 à L/2 dans notre cas.
Donc c'est parce que l'exercice nous a imposé la position du point M origine du repère qu'on a puis trouver dire que P varie -L/2 à L/2: Ceci est donc un cas particulier.
Dans le cas où le fil est infini, utiliser t-on toujours dOP ou dL puisque L n'est plus une constante puisqu'il est à l'infini?
Vous aviez écris:<<Le théorème de Gauss n'est pas applicable de façon simple...Cela n'est vrai que pour le fil de longueur infinie.>>: Dans notre cas, je pense que l'exercice nous oblige à créér le champ en une position fixe qui sera l'objet d'étude de symétrique. Et là, nous pouvons trouver la même direction pour le champ(normal à la surface du cylindre en ce point). Je pense donc qu'on peut alors utilisé le théorème de Gauss dans notre cas.
Ainsi si je comprend bien ce que vous voulez me faire comprendre, pour d'autre exercices qui ne vont pas présenter des particularités, il est impossible de calculer le Champ en utilisant le théorème de Gauss car le théorème de Gauss a des contraintes pour son utilisation.
D'accord avec ce que tu écris dans tes deux premiers paragraphes.
Dans le cas où le fil est infini, utiliser t-on toujours dOP ou dL puisque L n'est plus une constante puisqu'il est à l'infini?
C'est bien la mesure algébrique de OP qui varie de -
 à +
à + . L n'est plus définie, c'est une grandeur qui temps vers l'infini.
. L n'est plus définie, c'est une grandeur qui temps vers l'infini.
Je pense donc qu'on peut alors utilisé le théorème de Gauss dans notre cas.
Le théorème de Gauss appliqué à un cylindre de hauteur h quelconque demande de calculer le flux à travers la totalité de la surface fermée, ce qui suppose de connaître les caractéristiques du vecteur champ en tout point de la surface du cylindre, pas seulement dans le plan médiateur. Si le fil n'est pas de longueur infinie, le vecteur champ n'est pas en tout point de la surface latérale, normal à cette surface : complication dans le calcul du flux ; il n'est pas non plus de norme constante en tout point de cette surface ; bref : le calcul du flux pour un cylindre de longueur finie est impossible de façon littérale. Le théorème de Gauss est donc en pratique inutilisable dans ce cas.
Je comprend parfaitement.
Vous m'aviez écris :
<<Il n'est pas non plus astucieux d'avoir noté x la distance OM tout en notant dEy la composante du vecteur champ colinéaire à OM mais après tout>>
Par là je comprend que vous approuvez la figure que j'ai fais et qu'une telle figure est accepté conformément aux lois mathématiques. Cependant la figure est loin d'être avantageux, facile pour faire une bonne résolution du problème.
J'aimerais bien que vous m'aider à comprendre la raison pour laquelle cette représentation n'est pas astucieux et à améliorer la figure que j'avais représenté dans le but de résoudre le problème posé.
Le fait de noter x la distance OM alors que le vecteur est colinéaire à l'axe des abscisses n'est pas très astucieux.
De façon plus générale, en particulier lorsqu'il faut raisonner sur les symétries et les invariances de la source pour savoir si l'usage du théorème de Gauss est possible ou non, il est pertinent d'utiliser un système de coordonnées en accord avec les symétries de la source : coordonnées cylindro-polaire (on dit aussi cylindriques) si la source présente un axe de symétrie, coordonnées sphériques si la source présente un centre de symétrie.
Le document référencé ci-dessous pourra peut-être t'aider ; Les parties I et II traitent de l'influence des plans de symétrie ou d'antisymétrie passant par le point M où on cherche à déterminer le vecteur champ électrique. Je pense que tu as compris l'essentiel.
Le paragraphe VII fournit des schémas adaptés aux sources présentant un centre de symétrie ou un axe de symétrie.
![]()
Je n'arrive pas à accéder aux documents (Quand j'appuie sur ce qui est en bas, rien ne se passe).
En ce qui concerne la figure que j'ai faite, le vecteur OM n'est pas colinéaire à l'axe des abscisses comme vous le prétendez. De plus c'est l'exercice qui a dit que le champ est créé à une distance x sur la médiatrice du fil.
Il aurait été préférable alors de permuter l'axe des x et l'axe des y de façon que la distance x ne soit pas mesurée le long de l'axe des y !
Bizarre pour le fichier lié. Je réussis à l'ouvrir à la fois sur mon ordinateur et sur mon téléphone portable.
À voir ce que vous venez dire par écrit, il faut que je transforme l'axe que j'avais considéré comme celui des abscisses en celui des ordonnés puis celui des ordonnés en celui des abscisses (une permutation des axes).
Dommage qu'il m'est impossible de consulter ce document, un document qui m'apporterait encore davantage.
Voici ma proposition de réponse après avoir suivie vos conseils.
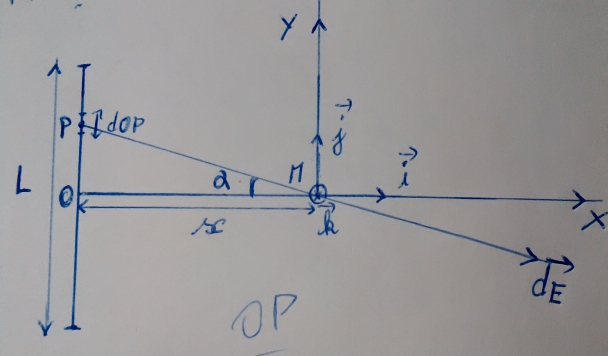
1- Trouvons l'expression du champ électrostatique en M situé à une distance x sur la médiatrice du fil de longueur L.
dE( dOPvecPM)÷(4
dOPvecPM)÷(4
 oPM³) avec
oPM³) avec  dOP=dq
dOP=dq
- Étude de symétries.
*Plans de symétries :
Ce sont: (M, ,
, ) et (M,
) et (M, ,
, )
)
D'où le vecteur E est orienté suivant l'axe OX.
- Étude d'invariance
*Par translation suivant l'axe OY, la distribution de charge(soit une abscence de Charges le long de l'axe) est uniforme. Alors Le champ E n'est pas en fonction de y.
* Par translation suivant l'axe OZ, la distribution de charge(soit une abscence de Charges le long de l'axe) est uniforme. Alors Le champ E n'est pas en fonction de z.
*Par translation suivant l'axe OX, la distribution de charge(soit une variation de Charges le long de l'axe) n'est pas uniforme. Alors Le champ E est en fonction de x.
•On conclut que le champ E est uniquement en fonction de la variable x.
vecE=Ex
dEx=(  dOP×PMx)÷(4
dOP×PMx)÷(4
 oPM³)
oPM³)
On a:
*PMx=x et PM³=x³÷cos³
*tan =OP÷x
=OP÷x dOP= x(1+tan²
dOP= x(1+tan² ) car x est une constante.
) car x est une constante.
Alors:
dEx=( cos
cos d
d )÷(4
)÷(4
 ox)
ox)
 Ex=
Ex= dEx=[(
dEx=[( )÷(4
)÷(4
 ox]
ox] cos
cos d
d (
( variant de-
variant de- à
à  )
)
Donc Ex=( sin
sin )÷(2
)÷(2
 ox) et
ox) et
vecE=Ex =(
=( sin
sin )
) ÷(2
÷(2
 ox)
ox)
2- Disons ce que deviennent ces expressions quand le fil est infini?
1er cas: L
 i.e. OP
i.e. OP 
 .
.
On sait que sin =(OP÷PM)
=(OP÷PM)
or PM=(OP²+x²)½ (D'après la propriété de Pythagore dans le triangle rectangle OPM)
Alors sin =OP÷(OP²+x²)½
=OP÷(OP²+x²)½
Quand L
 , OP
, OP
 et donc sin
et donc sin
 1.
1.
Comme Ex=( sin
sin )÷(2
)÷(2
 ox), elle deviendra Ex=(
ox), elle deviendra Ex=( )÷(2
)÷(2
 ox) et VecE=Ex
ox) et VecE=Ex =(
=( )
) ÷(2
÷(2
 ox) si le fil est infini.
ox) si le fil est infini.
Tout cela me semble correct. Une précision tout de même.
L'étude des plans de symétries est utile dans tous les cas, que le fil soit de longueur finie ou de longueur infinie.
En revanche, l'étude des invariances n'est utile que pour savoir si le théorème de Gauss est applicable. Quand tu conclus :
On conclut que le champ E est uniquement en fonction de la variable x.
Cela est valide uniquement si le fil est de longueur infinie. Sinon, ma direction et la norme du vecteur champ dépendent à la fois de x et de y.
2eme cas: en variant  entre -π÷2 et π÷2, on retrouve le même résultat.
entre -π÷2 et π÷2, on retrouve le même résultat.
3- Composons au résultat obtenu en utilisant le théorème de Gauss.
Cas où le fil est infini.
Prénons comme surface fermée un cylindre d'axe la ligne infini de rayon x.
Par raison de symétries et d'invariance le vecteur E est uniquement en fonction de x ; est colinéaire au vecteur normal de la surface latérale et sortant.
Le flux du vecteur E sortant de la surface fermée est:
 (vecE)=
(vecE)=  (vecEL)+
(vecEL)+ (vecE1)+
(vecE1)+ (vecE2).
(vecE2).
Le flux des vecteurs E1 et E2 sont nulles car la normale en ces surfaces sont perpendiculaires aux vecteurs vecE.
 (EL)=
(EL)=
 SL (VecE.Vecn.dSL= E2πxh
SL (VecE.Vecn.dSL= E2πxh
La charge totale contenue dans la surface fermée étant Q=  h, on a:
h, on a:
Ex= ÷(2
÷(2
 ox) et VecE=Ex
ox) et VecE=Ex =(
=( )÷(2
)÷(2 ox).
ox).
Vous aviez écrit :<<Cela est valide uniquement si le fil est de longueur infinie. Sinon, ma direction et la norme du vecteur champ dépendent à la fois de x et de y.>>
Je n'arrive pas à comprendre puisque après avoir fait l'étude d'invariance et si la distribution de charge est uniforme, on dit que le vecteur ne dépend pas de la variable ; puis si la distribution n'est pas uniforme, le vecteur dépend donc de la variable en question.
C'est cette propriété que je prétend utilisé et je pense avoir donné les résultats en fonction des exigences de cette propriété.
Le fait que vous avez dit que E peut dépendre de x et y pour le fil fini et de x pour le fil infini puis en même temps moi je trouve autre chose en utilisant la propriété me rend un peu "bouleversé".
Imagine un point M à la distance x du fil mais n'appartenant plus au plan médiateur du fil. Le plan contenant M et perpendiculaire au fil ne serait plus un plan de symétrie. Le vecteur champ en M n'appartiendrait plus à ce plan : il aurait une composante suivant x et une composante suivant y. De plus, le calcul de ces deux composantes seraient mathématiquement très compliqué.
Pour conclure je dirai que pour un fil fini chargé créant de champ en importe quel point de l'espace, le champ E n'est pas uniforme en tout pointt de l'espace autrement dit il n'a pas les mêmes propriétés en tout point de l'espace c'est dire que sa direction ne demeure pas constante en tout point de l'espace.
Cependant pour notre cas ci, l'exercice nous oblige à créer le champ sur la médiatrice du fil(ce qui appartient au plan médiateur du fil) et ainsi le champ est bien uniquement suivant l'axe OX.
De plus, ce n'est pas ce que vous m'aviez reproché "plus haut"(En éffet vous m'aviez reproché le fait que l'expression du champ n'est pas uniquement en fonction de x.) Or c'est l'utilisation de la règle d'invariance qui m'a permis de retrouver un tel résultat.
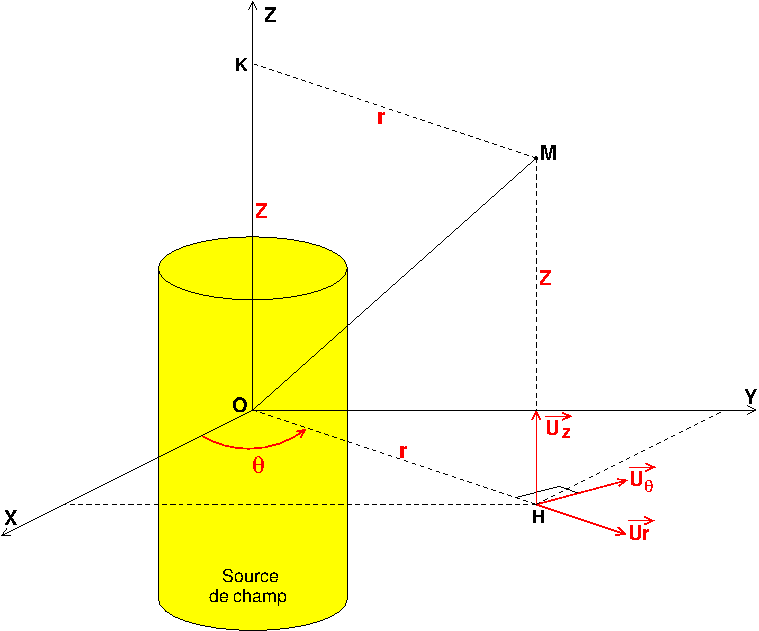
Je raisonne en coordonnées cylindriques, beaucoup plus pratique pour étudier les symétries et les invariances.
Pour un fil de longueur finie :
Invariance par rotation autour de l'axe Oz donc le vecteur champ ne dépend pas de la variable  mais dépend des variables r et z.
mais dépend des variables r et z.
Le plan contenant M et l'axe du fil est plan de symétrie donc la composante E du vecteur champ est toujours nulle. On Obtient donc, pour un point M quelconque :
du vecteur champ est toujours nulle. On Obtient donc, pour un point M quelconque :
avec des composantes Er et Ez qui dépendent toutes les deux des variables r et z ! Rien de simple.
La situation se simplifie si on se limite à des points M appartenant au plan médiateur (Oxy). Il existe alors un second plan de symétrie : le plan (Oxy) et alors :
avec une composante Er qui ne dépend que de la variable r.
Pour le symétrie, j'ai compris puisqu'on ne peut se UE trouver un seul plan de symétrie.
À voir ce que vous venez de me montrer, j'aurais croire que pour l'étude d'invariance, vous n'avez utilisé que le cas de "rotation". C'est comme si "la translation" ne devrait pas être fait(Et c'est à ce niveau que je n'arrive pas à comprendre.)
En éffet par translation suivant l'axe OZ, il a aussi invariance selon moi, donc on supprime z aussi de l'expression de E. Ensuite par translation suivant l'axe dirigé par vecEr, il n'y a pas d'invariance donc E est uniquement en fonction de r.
Je ne sais pas si la compréhension si que j'ai de la notion d'invariance est fausse.
Il y a invariance par translation suivant z seulement si le fil est de longueur infinie.
En effet , pour le fil de longueur finie, le long de l'axe des z :
 >0 si : -L/2
>0 si : -L/2  z
z  L/2
L/2
 =0 si z<-L/2 et si z>L/2.
=0 si z<-L/2 et si z>L/2.
C'est peut-être cela qui, depuis le début, te gêne.