Electromagnetisme, exercice de Physique

 Niveau licencePartager :
			        
Electromagnetisme
Posté par 
bissinyandoup  15-10-17 à 20:06
Bonsoir! 

S'il vous plait j'ai rencontré un probleme sur cet exercice et j'aimerais avoir de l'aide s'il vous plait

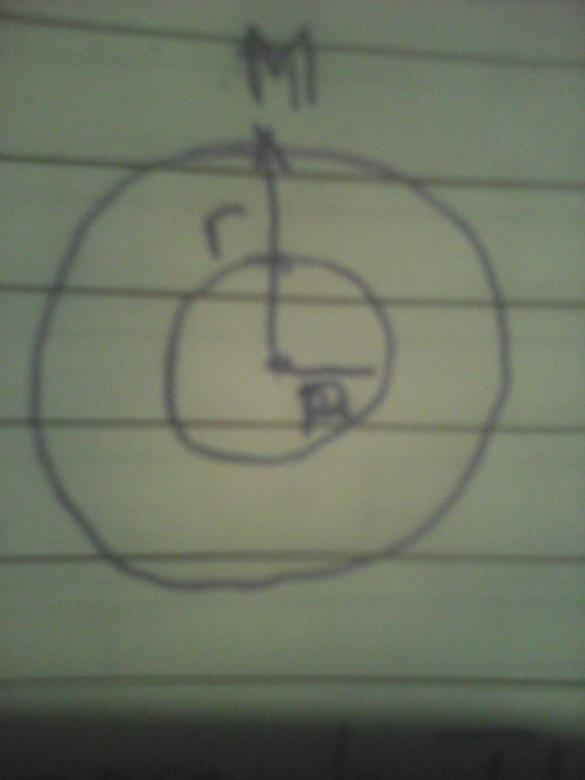
On considere une sphere (S)  de centre O et de rayon R,  chargée en surface de densité volumique  uniforme.  Calculer le champ electrostatique, puis le potentiel et l'energie electrostatique  en tout point M de l'espace. 
 Posté par 
diracre : Electromagnetisme  15-10-17 à 20:09
Hello

Citation :
chargée en surface de densité volumique 

N'es tu pas en train de traiter 2 problèmes à la fois? 
 Posté par 
diracre : Electromagnetisme  15-10-17 à 20:10
Mais quoiqu'il en soit, le Théorème de Gauss devrait pouvoir te servir
 Posté par 
bissinyandoupre : Electromagnetisme  15-10-17 à 20:21
La densite  etant constante,  j'ai

=dq/d

Pour r>R , d'apres le theoreme de gauss,  j'ai

=E. nds=Qint/0. Je considere donc que la sphere est uniformement chargé c'est a dire =E. S =4r2E et Qint=V=4/3 R3 tout calcul bien fait je trouve

E=R3/30r2.

Pour r=R je remplace R dans sa relation precedente et j'ai E=r/30

Pour r<R,  j'ai été tenter de dire que E=0 mais je, doute.  Aidez moi s'il vous plait. 
 Posté par 
bissinyandoupre : Electromagnetisme  15-10-17 à 20:26
Voila mon schemas

 Posté par 
diracre : Electromagnetisme  15-10-17 à 20:39
ben ... Quelle est la charge à l'intérieur d'une sphère de rayon r ???
 Posté par 
bissinyandoupre : Electromagnetisme  15-10-17 à 20:41
C'est donc ce que je ne sais pas dirac
 Posté par 
diracre : Electromagnetisme  15-10-17 à 22:59
La sphère de rayon r a pour volume

Donc la charge que contient cette sphère est:  

Et maintenant tu appliques le Th. de Gauss à cette sphère.
 Posté par 
bissinyandoupre : Electromagnetisme  15-10-17 à 23:03
Donc ce, que j'ai fait n'est pas bon? 
 Posté par 
diracre : Electromagnetisme  15-10-17 à 23:13
???

Pour e<R

et 

Gauss te dit alors 

Je te laisse finir?
 Posté par 
bissinyandoupre : Electromagnetisme  15-10-17 à 23:18
Je vois.  J'aimerais dinc savoir quand est ce le champ peut etre nul dans une sphere
  Posté par 
diracre : Electromagnetisme  16-10-17 à 06:28
Dans le cas d'une sphère chargée en surface uniformément, le champ en tout point (r<R) sera nul.