Bonsoir. Fais un schéma de la situation en représentant les différentes forces, notamment...

Tu as donc un fil accroché au plafond en P, qui pend, parcouru par un courant d'intensité I et soumis à un champ magnétique B uniforme.

Ton fil, lorsque l'état d'équilibre est atteint après la déviation (rotation autour du point P), est soumis à 3 forces : Son poids, la réaction du plafond et la force magnétique de Laplace.



Continue en utilisant donc le TMC (plus pratique que la RFD dans ce cas précis).

- C'est comme une expérience des rails de Laplace mais ton conducteur est vertical au lieu d'être horizontal -

Bonjour,
J'ai exactement la même question et j'aimerai quelques details suplémentaires pour les forces, et savoir comment utiliser le TMC.

Bonsoir,

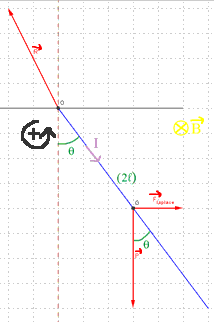
Pour les forces, voir le schéma joint... (choisit arbitrairement donc...)
J'ai volontairement remplacer P par O pour le point de pivot, afin de ne pas confondre avec le vecteur-poids .
Je choisis le sens trigo comme sens positif de rotation et des angles et je pose que le fil a une longueur égale à (2L)


TMC : La dérivée du moment cinétique est égale à la somme des moments des forces extérieures appliquée au mobile.
d/dt = ()

Ici, si on se place à l'équilibre, d/dt = = ^ + ^ + ^

L'avantage du TMC, c'est que ne fait pas tourner le fil étant donné que son point d'application est sur O.

En passant aux normes des produits vectoriels :
0 = L.mg.sin(OG;P) + L.ILB.sin(OG;F)
0 = L.mg.sin(-) + IL²B.sin(/2 - )
0 = -mgL.sin() + IL²B.cos()


C'est à dire, par transposition :
sin()/cos() = tan() = (ILB)/(mg)


- si je ne m'abuse -