Inscription / Connexion Nouveau Sujet
Electrocinétique - montage de plusieurs ALI
Bonjour,
J'ai calculer dans une question précédente les fonctions de transferts complexes des différentes ALI et j'ai trouvé:
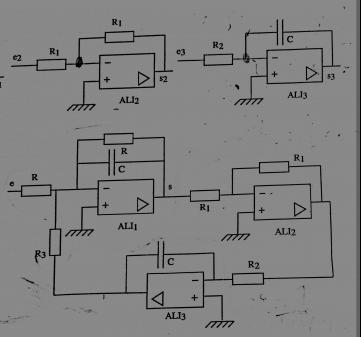
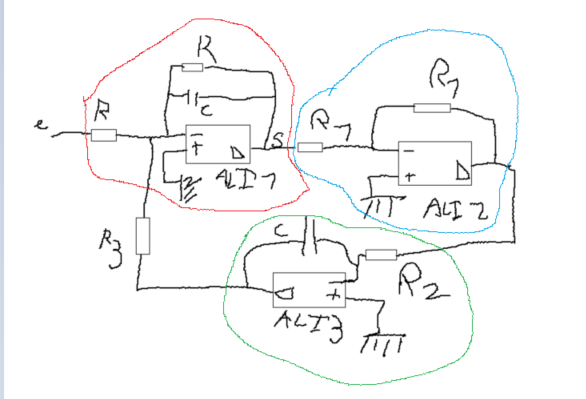
ALI 1 (entouré en rouge) : H1(jw)=-1/(1+jRCw)
ALI 2 (entouré en bleu) : H2(jw)=-1
ALI 3 (entouré en vert) :
H3(jw)=-1/(1+jR2Cw)
Ensuite on me demande de calculer la fonction de transfert de l'ensemble du circuit.
Le problème étant que je n'arrive absolument pas à trouver comment aborder cette question...
Pouvez-vous m'aider ? Merci d'avance
Bonsoir
Tu n'as pas précisé la sortie du montage. Je note s la tension de sortie de ALI2 :
Mais tu as aussi :
Attention : ce circuit n'est pas vraiment un filtre...
Oups ! Mon premier message suppose R3 reliée à e, ce qui ne semble pas être le cas mais alors je m'interroge : La sortie du montage n° 3 est maintenue au potentiel nul...
Tu ne pourrais pas scanner le montage fourni et le poster ici pour plus de clarté en fournissant un énoncé complet ?
Le règlement demande de scanner les schémas et de les poster. Pour l'énoncé, dans la mesure où tu avais commencé par résumer l'énoncé et par expliquer le travail déjà fait, pas de problème je pense. Avec un schéma plus clair, je me rends compte que mes premiers messages n'étaient pas très adaptés. Je recommence donc à zéro.
D'accord avec ton étude du circuit 2 :
En revanche, il te faut revoir ton expression de ; la partie 3 du montage correspond à un simple intégrateur inverseur.
Ensuite, puisque ”s” est la sortie de ALI1, : la fonction de transfert du montage. Ce n'est pas la valeur
que tu as obtenue à cause de la résistance R3. Méthode possible : appliquer le théorème de Millman à l'entrée E- de ALI1. Puisque ALI1 fonctionne en régime linéaire, le potentiel de E- est nul. Cela va te fournir une relation entre e, s, e3 qui permettra d'obtenir le résultat recherché.
Bonjour à vous deux,
Normalement ce n'est pas autorisé donc en espérant que je ne le fasse pas bannir
Pour l'énoncé, dans la mesure où tu avais commencé par résumer l'énoncé et par expliquer le travail déjà fait, pas de problème je pense
Attention, le règlement ne demande pas de résumer un énoncé (qui généralement est un exercice périlleux puisqu'on finit par en perdre son sens, voir ça vire au quiproquo) mais de le recopier intégralement ou de ne recopier que les 5 premières lignes selon les cas de figure :
 extrait de
extrait de Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Bonjour à vous deux,
Normalement ce n'est pas autorisé donc en espérant que je ne le fasse pas bannir
Pour l'énoncé, dans la mesure où tu avais commencé par résumer l'énoncé et par expliquer le travail déjà fait, pas de problème je pense
Attention, le règlement ne demande pas de résumer un énoncé (qui généralement est un exercice périlleux puisqu'on finit par en perdre son sens, voir ça vire au quiproquo) mais de le recopier intégralement ou de ne recopier que les 5 premières lignes selon les cas de figure :
[faq]image[/faq]

Très bien je ferais attention la prochaine fois
Le règlement demande de scanner les schémas et de les poster. Pour l'énoncé, dans la mesure où tu avais commencé par résumer l'énoncé et par expliquer le travail déjà fait, pas de problème je pense. Avec un schéma plus clair, je me rends compte que mes premiers messages n'étaient pas très adaptés. Je recommence donc à zéro.
D'accord avec ton étude du circuit 2 :
En revanche, il te faut revoir ton expression de
Ensuite, puisque ”s” est la sortie de ALI1,
Merci de l'aide je vais essayer

vanoise, j'ai donc essayer ce que vous m'avez proposé. J'ai donc appliqué le théorème de Millman à l'entrée - de l'ALI 1 comme il y avait un nœud juste avant avec R et R3 je l'ai également appliqué ici. En regroupant les deux expression j'arrive bien a quelque chose qui a la forme souhaitée mais je ne sais pas si c'est juste. Voici ce que j'ai trouvé :
H(jw) =
avec donc -H0=
a=CR et b=
Pouvez me confirmer que c'est bien cela ?
PS: j'avais mal recopier, j'ai H3 =
Le règlement demande de scanner les schémas et de les poster. Pour l'énoncé, dans la mesure où tu avais commencé par résumer l'énoncé et par expliquer le travail déjà fait, pas de problème je pense. Avec un schéma plus clair, je me rends compte que mes premiers messages n'étaient pas très adaptés. Je recommence donc à zéro.
D'accord avec ton étude du circuit 2 :
En revanche, il te faut revoir ton expression de
Ensuite, puisque ”s” est la sortie de ALI1,
Grosse erreur de calcul de ma part, j'ai finalement :