Inscription / Connexion Nouveau Sujet
Electrocinétique / complexe / RLC
Bonjour à tous,
Voila un petit exercice a résoudre sur lequel j'ai beaucoup de mal, je dois dire que le passage en complexe me perturbe un peu, et j'ai du mal à m'y habituer ....
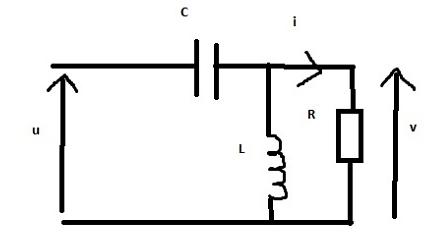
cf Image
Montrer que l'intensité qui circule dans R est indépendante de R si LC ²=1 avec
²=1 avec  la pulsation de u(t).
la pulsation de u(t).
Quelle est la valeur correspondante de i ?
J'ai donc u(t) = Um cos ( t) ---------------> Um exp(j
t) ---------------> Um exp(j t)
t)
J'ai essayé de calculer l'impédance équivalente aux bornes du générateurs, mais complètement inutile puisque je cherche i aux bornes de R ...
Je pensais faire une loi des noeus, avec i1 l'intensité au condensateur, et i2 a la bobine: i = i1 - i2
Ensuite je sais que i2= v / jl w, de meme i1 = u * jc
w, de meme i1 = u * jc . Mais je suis bloqué puisque je n'ai pas v ...
. Mais je suis bloqué puisque je n'ai pas v ...
A vrai dire je suis un peu perdu, une petite piste serait la bienvenue.
Désolé pour la qualité du schéma, j'ai pas d'image disponible.
Merci à tous
Désolé pour le multi post, mais je viens de me rendre compte que mon image etait trop grande et n'a pas ete prise en compte.
Je ne peux modifier mon premier message, donc je rajoute un message, si un modo passe par la, et qu'il peut fusionner mes messages, un grand merci a lui =)
Bonsoir,
Il suffit d'écrire la loi des mailles en complexe :
D'où it...
it étant le courant total dans le circuit
Ensuite, pour trouver iR, il suffit d'appliquer le diviseur de courant.
Oui pour it sauf que je l'écris :
mais c'est la même chose...
Ensuite, je suis d'accord avec iR mais je l'écris avec les impédances à des fins de simplification :
Mais avec les admittances, on y arrive aussi...
Et, ensuite, il faut remplacer LC 2 pa
2 pa
J'ai posté par accident  ...
...
Et, ensuite, il faut remplacer LC 2 par 1 et
2 par 1 et par
.
Et on trouve :
sauf erreur éventuelle...
R // wL : Z = jwLR/(R+jwL)
Ztotal vue de l'entrée = (1/(jwC)) + jwLR/(R+jwL)
Ztotal = (R + jwL+ jwLR.jwC)/[jwC.(R+jwL)]
Ztotal = (R - w²LRC + jwL)/[jwC.(R+jwL)]
v/u = Z/Ztotal
v/u = jwLR.jwC.(R+jwL)/[(R+jwL).(R - w²LRC + jwL)]
v/u = -w²LRC/(R - w²LRC + jwL)
v/u = -w²LRC/[R(1 - w²LC) + jwL]
et i(R) = v/R -->
i(R) = -u.w²LC/[R(1 - w²LC) + jwL]
Et si w²LC = 1 --->
i(R) = -u.w²LC/(jwL) = u.jwC/L = u.j.(1/racine(LC)).C/L
i(R) = u.j.racine(C/L) ... indépendante de R.
... analogue à la réponse de Marc35
-----



