Bonsoir bonsoir, j'ai besoin d'aide pour le problème suivant;

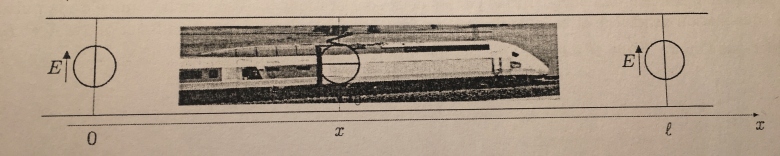
« Longtemps après son démarrage, on peut supposer que le TGV fonctionne en régime permanent. La puissance électrique nécessaire à son fonctionnement est fournie au TGV à partir de sous-stations électriques implantées tout le long de la voie et espacées d'une distance l= 60 km. Elles sont reliées par un fil conducteur, la caténaire, suspendu au-dessus des rails. La motrice TGV reçoit l'alimentation de la caténaire par un contact glissant appelé pantographe sur son toit. Tous les moteurs électriques de la locomotrice sont montés en parallèle entre le pantographe et les rails qui servent de liaison masse à la Terre, conformément au schéma ci-dessous.
Voir photo en dessous

Les sous-stations électriques seront assimilées à des générateurs idéaux de f.é.m. E constante et identique pour toutes les sous-stations.

On admettra que les moteurs de la locomotive se comportent, d'un point de vue électrique, de la même manière qu'un générateur idéal de courant, imposant un courait lo constant orienté de la caténaire vers le sol comme vUE lo schéma ci-dessus.

Le mardi 3 avril 2007, à 13h14, la SNCF, associée à la compagnie ALSTOM, portait le record du monde de vitesse sur rail à la valeur 574, 8 km.h^-1 au point kilométrique 194 de la ligne à grande vitesse est-européenne. Lors du record de vitesse, la puissance des moteurs était augmentée par rapport aux moteurs habituels et la tension d'alimentation en sortie des sous-stations avait été montée exceptionnellement à E=31,2kV sur la zone du record à la place des 25kV habituels. Au moment du record, l'intensité électrique reçue au pantographe a été mesurée : elle était de I₀= 800 A.

Pour l'étude qui va suivre, on s'intéresse au trajet du train entre deux sous-stations. On supposera que la section transverse de la caténaire (surface transversale du fil) est de s = 1, 47 cm². La caténaire est en cuivre, métal dont. la conductivité est de =5, 82.107 ^-1.m^-1.

Le rail rectiligne est confondu avec l'axe (Ox) dont l'origine O (x= 0) est placée au niveau de la sous-station à gauche sur le schéma. La variable x [0, l] repère à tout instant la position de la locomotive entre les deux sous-stations d'alimentation (voir le schéma en début d'énoncé).

Une longueur e de rail est équivalente à un conducteur ohmique de résistance R=l/s .

Nous allons chercher tout d'abord à justifier que le rail peut être modélisé par un simple fil de résistance nulle.


Q1. Évaluer approximativement la surface de section s_raild'un rail de chemin de fer, en cm²?

Q2. En considérant que le rail est fait du même métal que la caténaire (donc même valeur de conductivité), justifier que l'on puisse négliger la résistance du rail devant celle de la caténaire (que l'on notera R dans la suite).

Q3. Déterminer la résistance totale R de la caténaire entre les deux sous-stations considérées et effectuer l'application numérique.

Q4. Donner l'expression de la résistance R₁de la portion de caténaire amenant le courant à la locomotive depuis la sous-station de gauche. On exprimera d'abord R₁en fonction de , s et x et/ou l, puis on réexprimera le résultat en fonction de R, l et x (on rappelle que R désigne la résistance totale de la caténaire entre les deux sous-stations).

Q5. Même question pour R₂, résistance électrique de la portion de caténaire amenant le courant à la locomotive depuis la sous-station de droite, que l'on réexprimera en fonction de R, l et x.

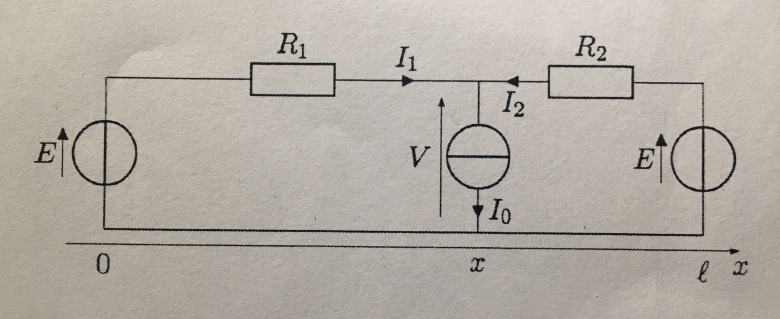
Le système électro-mécanique étudié est donc équivalent au circuit électrique ci-dessous.
Voir prochain poste

Q6. Etablir les expressions de I₁, I₂ (lire i1 i2) et V en fonction de E, I₀, R₁et R₂, puis en fonction de R, E, I₀,x et l. On utilisera pour cela les lois nécessaires pour établir un système d'équations, avec autant d'équations que d'inconnues, que l'e résoudra.

Montrer, notamment, que I₁=I₀((l-x)/l) .

Q7. En déduire la puissance consommée P_c consommée par la locomotive (c'est-à-dire reçue par la locomotive) en fonction de E, R, I₀, x et l.

Q8. Déterminer la puissance P_j reçue par la caténaire, c'est-à-dire la somme de la puissance reçue par R₁ et par R₂fonction de R1, I₁, R2, I2, puis en fonction de R, I₀, x et l. Que devient l'énergie associée?

Q9. Déterminer la puissance totale P_f fournie par les deux sous-stations (c'est-à-dire la somme de la puissance four par la sous-station de gauche et celle de droite), en fonction de E, I₁et I₂, puis en fonction de E et I₀.

Q10. Vérifier que l'on a : P_f=P_j+ P_c.
Que signifie physiquement cette égalité? »

J'ai essayé de faire la question 1 à 4 mais je ne suis pas sûr de mes résultats;

Q1. Je dis que les dimensions conventionnelles d'un rail de TGV sont;
L=2,6m, l=25cm, h=15cm.

Donc s_rail=25*15=375 cm².

2) On suppose que _rail=_caté

On sait que s_caté=1,47cm²

Donc s_caté<<s_rail car 1,47<<375
D'après l'énoncé R=l/s

Donc pour une même longueur l donnée:
R_caté>>R_rail.

Q3. On note R la résistance de la caténaire.

Entre les deux sous-stations, on a:
l=60km

Or, R=l/s

A.N: R=^-1.m^-1.

Q4. Notons x₁ la distance entre la sous station de gauche et la resistance R₁.

Alors R₁=x₁/s

On pose x₀=l-x₁>0 (car l>x₁)

Donc R₁=(l-x₀)/s=R-x₀/s... je pense que c'est faux.

MERCI À VOUS POUR VOTRE AIDE (Désolé c'est un peu long)!