Inscription / Connexion Nouveau Sujet
Electricité : valeur moyenne
Bonjour à tous,
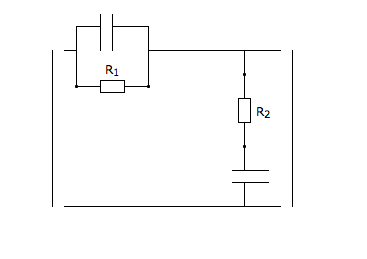
J'ai un exercice qui porte sur un filtre (voir fichier joint). Dans les premières questions, j'ai calculé sa fonction de transfert et représenté l'allure de sa courbe de gain. On applique au circuit un signal V1(t) sinusoïdal qui oscille entre les valeurs aE et 3aE autour de 2aE (a sans dimension, E homogène à une tension).
1) donner l'expression de V1(t).  ---> V1(t)=2aE+aE*sin(2
---> V1(t)=2aE+aE*sin(2 /T *t)
/T *t)
2) V2(t) est de la forme (admis) V2(t)=<V2> + V2m*sin(2 Pi/T *t +
Pi/T *t +  ).
).
-Exprimer la valeur moyenne <V2> su signal.
-Exprimer l'amplitude V2m de la composante alternative de V2(t) en fonctionde a, E,  , et T. (
, et T. ( intervient dans l'expression de la fonction transfert)
intervient dans l'expression de la fonction transfert)
Voilà, je suis bloquée au niveau de la la question 2), je vous remercie de votre aide 
Le système étant linéaire, tu peux étudier la réponse aux différentes composantes du signal d'entrée prises séparément (une composante continue et une composante sinusoïdale) en appliquant le principe de superposition.
En conséquence:
-pour obtenir la valeur moyenne de , il faut appliquer la fonction de transfert à la composante continue de
.
-pour obtenir l'amplitude de sa composante alternative, il faut appliquer la fonction de transfert à la composante alternative de .
Merci pour votre réponse
-pour obtenir la valeur moyenne de V2(t), je peux donc écrire <V2>/2aE=fonction de transfert
-pour obtenir l'amplitude de sa composante alternative, j'aurai (V2m*ej(2 /T*t+
/T*t+ )) / (aE*ej(2
)) / (aE*ej(2 /T*t)) = fonction de transfert
/T*t)) = fonction de transfert
Merci de me corriger si j'ai fait une erreur
Le problème c'est que je ne voie pas comment il est possible que <V2>/2aE = (V2m*ej(2/T*t+)) / (aE*ej(2/T*t)) = fonction de transfert = V2/V1 ?
Et si je résouds, j'obtiens V2m en fonction de  qui n'est pas une donnée de l'énoncé donc impossible à calculer
qui n'est pas une donnée de l'énoncé donc impossible à calculer 
Merci d'avance pour vos réponses
On t'a demandé précédemment de calculer une fonction de transfert qui doit s'exprimer en fonction de la fréquence du signal appliqué en entrée. C'est peut-être le bon moment de l'utiliser...

Oui, j'ai utilisé mon résultat et j'ai voulu résoudre (V2m*ej(2 /T*t+
/T*t+ )) / (aE*ej(2
)) / (aE*ej(2 /T*t)) = (1+
/T*t)) = (1+
 )*(1+10*
)*(1+10*
 )/((1+1*5
)/((1+1*5
 )*(1+50
)*(1+50
 )) avec w=2
)) avec w=2 f = 2
f = 2 /T.
/T.
Mon problème est que je ne peux simplifier que par ej(2 /T*t) donc il me reste un ej
/T*t) donc il me reste un ej inconnu .
inconnu .
Une autre question : est-ce que la notation complexe pour V1(t) par ex est bien V1=2aE + aE*ej(2 /T*t) ou alors =2aEj + aE*ej(2
/T*t) ou alors =2aEj + aE*ej(2 /T*t)
/T*t)
Merci
On te demande de calculer "l'amplitude de la composante alternative" de . Il faut donc que tu calcules le module du signal complexe obtenu par application de la fonction de transfert. La phase disparaît.
Concernant la notation, pour être cohérent c'est la deuxième expression qui convient et le signal réel correspond alors à la partie imaginaire du signal complexe. Mai ça n'a en réalité pas beaucoup d'importance.
donc <V2> = 2aE*(1+2
 /T)(1+10*2
/T)(1+10*2
 /T)/ ((1+1/5*2
/T)/ ((1+1/5*2
 /T)*(1+50*2
/T)*(1+50*2
 /T))
/T))
et de la même façon V2m = aE*(1+2
 /T)(1+10*2
/T)(1+10*2
 /T)/ ((1+1/5*2
/T)/ ((1+1/5*2
 /T)*(1+50*2
/T)*(1+50*2
 /T))
/T))
Il n'y a donc qu'un facteur 2 entre les 2 résultats comme pour V1. Coïncidence ?
...ou grossière erreur? 
La fonction de transfert ne dépendrait-elle pas de la fréquence du signal d'entrée?
En particulier, que vaut et par suite
) lorsque le signal d'entrée est continu?
Tu ne peux pas appliquer la même fonction de transfert à deux signaux dont les fréquences sont différentes...
Je ne comprends pas pourquoi vous dîtes que les 2 signaux ont des fréquences différentes alors que dans leurs expressions c'est toujours la même période T qui intervient...?
Je viens de m'apercevoir d'une première erreur : mon expression de la fonction de transfert dépend de j et je les ai oubliés donc c'est H(jw)=(1+
 j)(1+10*
j)(1+10*
 j) / ((1+1*5
j) / ((1+1*5
 j)(1+50
j)(1+50
 j)) avec w=2
j)) avec w=2 f=2
f=2 T
T
Pour ce qui est de f, je ne vois que f=1/T
Le principe est de séparer le signal d'entrée en une composante continue
et une composante alternative
et d'étudier ensuite la réponse du circuit pour chacun d'entre eux.
Tu ne peux pas dire que ces signaux ont la même fréquence, si?
Non en effet je pensais qu'il s'agissait des composantes alternatives du signal d'entré et de sortie .
J'ai à présent bien compris le principe mais hélas je vois difficilement comment passer à la pratique ; peut-être n'ai-je pas une idée assez claire de ce qu'est une fonction de transfert et à quoi peut-elle servir ... Peut-être faut-il appliquer la fonction de transfert à <V1(t)> pour obtenir <V2(t)> donc calculer H(2aE) ?
Non, la fonction de transfert correspond au rapport entre signal de sortie et signal d'entrée, pour une fréquence donnée.
On a donc
et
avec la fréquence de la composante alternative de
.
D'où .



