Niveau école ingénieur

électricité triphasé

Posté par
machin70 14-05-19 à 21:54

Bonsoir,

J'ai un problème pour la résolution d'un exercice.

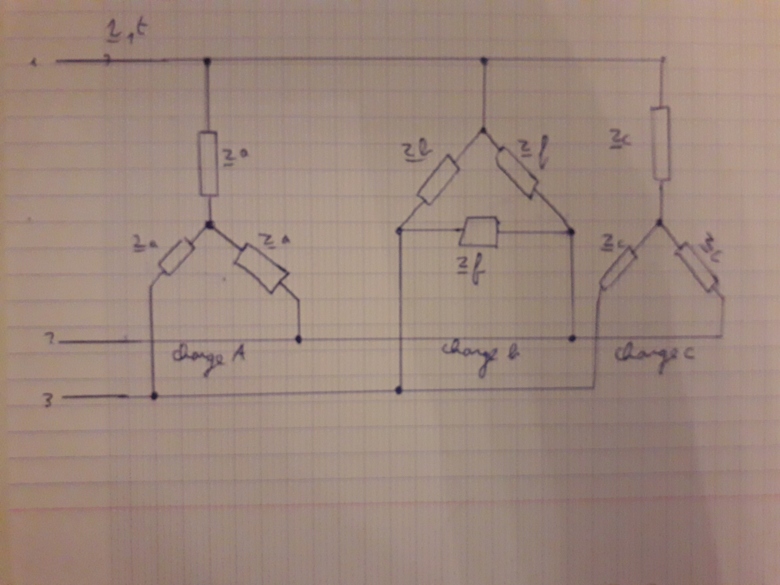
On considère la charge triphasée de la figure ci-dessous qui est alimenté par un réseau 220V/380V-50Hz; Les 3 charges sont équilibrées et ont pour impédences :

Z_a=(30-j18)
Z_b=(9,6-j12,6)
Z_c=(j16)

1) Quelle est la puissance active absorbée par le récepteur n°1?

2)Quelle est l'intensité totale I_1t absorbée sur la phase n°1 de la ligne d'alimentation par l'ensemble des trois charges?

1) U=RI I=U/R
P=UI*cos

P=U²/R*cos

$P=\frac{380^{2}}{30-18j}*\cos (-31)$

P=3.54KW

2) I_1t=I_a+I_b+I_c

$I_{t1}=\frac{380}{30-j18}+\frac{220}{5.33argument53.13}+\frac{380}{j44}=50.76A$

Pour la 1 le résultat me convient mais pour la 2 il ne correspond à aucun des 4 résultats proposés (c'est un qcm).

Où est mon erreur?

électricité triphasé

Posté par re : électricité triphasé 15-05-19 à 09:39

Salut,

Ton erreur : le déphasage entre 220 et 380 n'est pas nul !

C'est le moment d'appliquer Kennelly et de transformer tout en étoile...

Posté par re : électricité triphasé 15-05-19 à 13:20

Salut,

Alors pour Kennelly je suppose qu'il ne faut l'utiliser que pour le récepteur du milieu puisque les deux autres sont déjà en étoile?

Pour le récepteur du milieu j'ai donc Z_b=(9.6+12.8j)=16argument53.13°

Donc Je dois diviser cette impédance par 3 selon le théorème de Kennelly pour obtenir un montage en étoile ce qui donne Z_b/3=5.33argument53.13°

Pour le déphasage il est de 120° à 380V et de 90° à 220V

Calcul final : $\frac{380>120°}{30-18j}+\frac{\frac{380}{\sqrt{3}}>90°}{\frac{9.6+12.8}{3}}+\frac{380>120°}{44j}=46.13A$

Ce résultat ce rapproche des 45.9A annoncés.

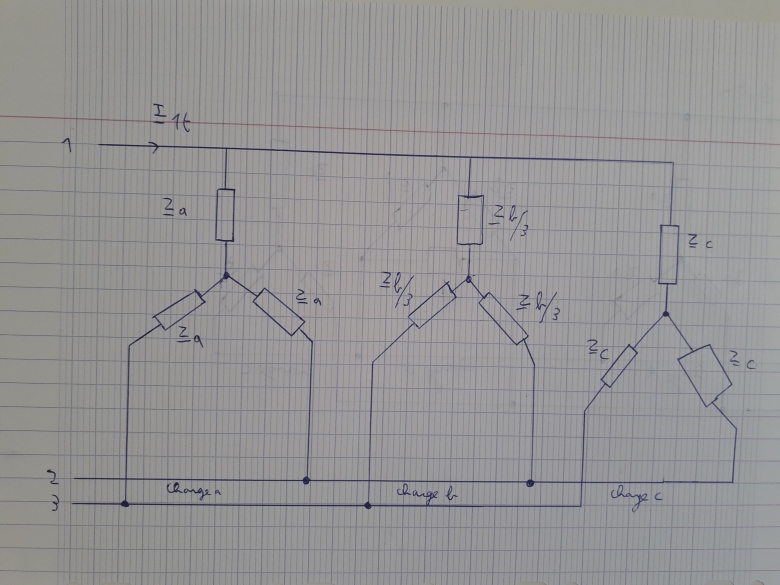
Je joins le schéma de la transformation par Kennelly

Merci beaucoup pour votre aide

électricité triphasé

Posté par re : électricité triphasé 15-05-19 à 15:49

La question 3 est : Quel est approximativement le facteur de puissance global de l'ensemble des trois charges?

La réponse est 0,66

Selon moi il faut se servir de la formule cos=P/S

Donc : S=U²/Z

$S=\frac{(380<120°)^{2}}{30-j18}+\frac{(\frac{300}{\sqrt{3}}<90°)^{2}}{\frac{9,6+j12,8}{3}}+\frac{(38<120°)^{2}}{44j}$

$P=\frac{(380<120°)^{2}}{30-j18}*cos(-30.96)+\frac{(\frac{300}{\sqrt{3}}<90°)^{2}}{\frac{9,6+j12,8}{3}}+*cos(53.13)\frac{(38<120°)^{2}}{44j}*cos(90)$

$cos\varphi =\frac{\frac{(380<120°)^{2}}{30-j18}+\frac{(\frac{300}{\sqrt{3}}<90°)^{2}}{\frac{9,6+j12,8}{3}}+\frac{(38<120°)^{2}}{44j}}{\frac{(380<120°)^{2}}{30-j18}*cos(-30.96)+\frac{(\frac{300}{\sqrt{3}}<90°)^{2}}{\frac{9,6+j12,8}{3}}+*cos(53.13)\frac{(38<120°)^{2}}{44j}*cos(90)}$

et cela ne donne pas 0.66

Posté par re : électricité triphasé 15-05-19 à 16:31

la question 4 : Quelle est approximativement la capacité unitaire des trois condensateurs à placer en triangle pour relever le facteur de puissance de l'ensemble des trois charges à 0.98?

$C=\frac{Q/3}{V_{c}^{2}*\omega }\Leftrightarrow C=\frac{(UIcos\varphi )/3}{V_{c}^{2}*\omega }$

AN : $C=\frac{(380*45.9*0.66)/3}{380^{2}*314}=128\mu F$

Bon alors je trouve 138F au lieu de 128F. Est-ce du au fait que le cos est égal à 0.98 et non 1?

Qestion 5 : Le facteur de puissanceétant remonté à 0.98 quelle est la puissance réactive de la charge b?

$Q_{1}=UIcos\varphi$

AN : $Q_{1}=380*45,9*cos(0.98)=17.44kVAR$ au lieu de 21.66kVAR selon le corrigé

Posté par re : électricité triphasé 15-05-19 à 17:19

machin70 @ 15-05-2019 à 15:49

... et cela ne donne pas 0.66

J'ai bien du mal à comprendre ce que tu fais avec les tensions... 380, 300, 38 (?).
Les charges étant équilibrées et prises en compte en étoile, tu peux simplement :
- relier les 3 points neutres ;
- appliquer la tension 220 entre phase et neutre ;
- faire le calcul des puissances en monophasé.
Le cos phi en mono sera évidemment le même que pour l'ensemble en 380.
Tu élimineras ainsi tes nouvelles erreurs de déphasage puisque c'est la tension 220V qui est prise comme seule et unique référence de phase (phase = 0).

Je te rappelle au passage que lorsqu'une impédance Z = r + jLw est branchée sous une tension V :
- la tension V (référence de phase) est en phase avec l'impédance complexe Z ;
- le courant qui traverse Z est en phase avec sa partie réelle r ;
- la puissance active r.I² est "en phase" avec le courant ;
- la puissance réactive (comptée >0) est "en phase" avec jLw ;
- la puissance réactive (comptée <0) est "en phase" avec -j/Cw ;
- la puissance apparente est "en phase" avec Z.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

électricité triphasé

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique