Inscription / Connexion Nouveau Sujet
electricité:Résistances équivalentes.
bonjour de laide svp
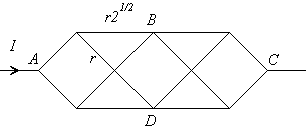
On considère un réseau électrique qui est un treillis métallique. Tous les côtés ont une résistance proportionnelle à la longueur.
Tu pourrais considérer que les points en regard de part et d'autre de l'axe AC, tels que les points B et D, sont au même potentiel.
Si les points de chaque paire (B et D pour la paire centrale) sont au même potentiel, on peut les relier par un conducteur de résistance nulle. Le réseau donné s'en trouve bien simplifié.
Sincérement je vois toujours pas là ou tu veu x en venir. sinon je comprends ce que tu me dis. mais je vois pas comment je pourrait retrouver la resistance équicalente
Mon idée est la suivante.
En appelant B'D', BD et B"D" les trois paires de points déjà considérées, le réseau peut se schématiser ainsi :
B' B B"
A o o o o C
D' D D"Si on fait passer un courant entre les points A et C, les points B' et D', B et D et B" et D" prennent respectivement, par raison de symétrie, un même potentiel. Les deux points de chaque paire peuvent donc être connectés l'un à l'autre, et le réseau devient
B'D' BD B"D"
A o o o o Cdont la résistance équivalente pet être aisément calculée.
Bonjour
Je pense que le résultat fourni par saturnelick est correct. Je me permets deux remarques.
1. La méthode proposée par Priam est bonne mais laisse en suspend le problème du calcul de la résistance équivalente entre B'D ' et BD et entre BD et B ''D''. La difficulté vient des noeuds situés sur l'axe de symétrie qui sont reliés à 4 résistances. Une astuce possible consiste à raisonner sur les symétries de répartition des intensités. On peut facilement montrer que le courant traversant une résistance r liée à un tel noeud passe intégralement dans la résistance située du même côté de l'axe de symétrie. Aucun courant ne traverse l'axe de symétrie. On peut donc calculer la résistance équivalente comme si les deux résistances r situées d'un côté de l'axe de symétrie étaient séparées des deux résistances r situées de l'autre côté de l'axe de symétrie.
2. La méthode peut se généraliser aux 4 noeuds situés sur l'axe de symétrie de sorte que le réseau est équivalent à deux sous réseaux en parallèle : celui situé au dessus de l'axe de symétrie et celui situé en dessous. Inutile alors d'appliquer la méthode de Priam. Si on note R la résistance équivalente à l'association de r en série avec l'association en parallèle (2r//r
2), on constate que le réseau est équivalent à une résistance 2R en parallèle avec une autre résistance 2R. La résistance équivalente au réseau est donc R.
Cela conduit bien au résultat de saturnelick.
Oui, après vérification, je confirme que le résultat de saturnelick est exact. On peut en simplifier l'écriture.
Je suis bien conscient que mon précédent message aurait été plus compréhensible accompagné de schémas mais je suis en ce moment en déplacement avec seulement un téléphone portable. À défaut, voici une référence d'exercice utilisant cette méthode.
Annuler
connectez vous