Inscription / Connexion Nouveau Sujet
Electricité niveau prepa
Bonjour,
j'ai un dm de physique-chimie avec une grosse partie d'électricité dessus
sur laquelle je bloque un peu.
il est divisé en deux grosse parties, voici l'énoncé :
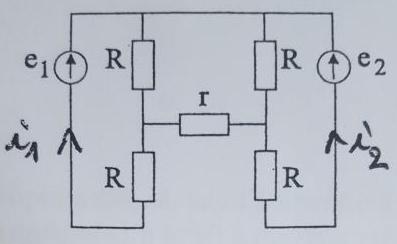
partie A: -établir pour les deux circuits l'expression littérale du courant i
partie B: -établir l'expression littérale du courant i1 et i2 traversant les générateurs e1 et e2
voici une photo des circuits:
1 photo: partie A
2 photo: partie B
3 photo: ce que j'ai fait pour la partie A (correction de faute possible)
merci de votre réponse à venir


Bonsoir,
Ce n'est pas très lisible tes propositions, tu devrais davantage utiliser ce qui est à disposition sur le forum :
le soucis c'est que ça fait vraiment de grosse grosse formule...
mais les voilà après loi des n?uds et lois des mailles, je tombe sur:
circuit 1 :
circuit 2 :
mais c'est vachement moins pratique et moins jolie...
et sur la deuxième partie je bloque totalement...
***Latex ajouté***
Bonjour gbm
Merci de prendre soin du confort des aidants !
Bonjour FloJ
Pour le circuit 1 : le théorème de Millman donne directement la tension commune U aux trois branches. Tu obtiens ensuite directement les intensités souhaitées. Sachant que les résistances sont toutes identiques, le calcul est très simple.
Pour le circuit 2 : Les lois des mailles et des nœuds semble le plus rapide : toutes les intensités peuvent s'exprimer en fonction de 3 inconnues i1,i2 et i à travers r. Loi des mailles ensuite...
Bonjour gbm
Merci de prendre soin du confort des aidants !
Bonjour FloJ
Pour le circuit 1 : le théorème de Millman donne directement la tension commune U aux trois branches. Tu obtiens ensuite directement les intensités souhaitées. Sachant que les résistances sont toutes identiques, le calcul est très simple.
Pour le circuit 2 : Les lois des mailles et des nœuds semble le plus rapide : toutes les intensités peuvent s'exprimer en fonction de 3 inconnues i1,i2 et i à travers r. Loi des mailles ensuite...
Bonsoir vanoise, j'ai eu le courage pour la deuxième, pour la première je me suis simplifié la vie

En fait le soucis pour les deux premiers circuits que j'ai omis de préciser (je suis désolé)
C'est qu'on est obligé d'utiliser les lois de Kirchoff d'où l'imposante ligne de calcul pour le premier calcul
et pour la deuxième partie, j'ai commencé par une équivalence thévenin-norton mais j'arrive pas à grand chose après....
Un peu d'aide pour le circuit 1. Si tu ne connais pas le théorème de Millman, tu peux retrouver la tension commune U commune aux trois branche en appliquant la loi des deux et en tenant compte de la loi d'Ohm. Cela donne :
puis :
Je te laisse terminer.
Pour le circuit 2, la même méthode conduit à :
puis :
Pour le circuit B, la loi des nœuds et des mailles est sans doute le plus rapide s'il s'agit de trouver i1 et i2. Si on se limite à l'intensité du courant dans r, le théorème de Thévenin peut donner plus rapidement le résultat.
en fait j'ai les bons résultats je pense mais je me suis fait ch*** a prendre des résistances R qui ne sont pas les mêmes donc forcement les choses deviennent d'un coup plus compliqué 
Pour la deuxième parti je suis passé sur du Norton c'est pour ça je pense que ça bloquait
Je remet tout ça au propre demain et je vous dit si je bloque sur autres choses, merci de vos réponses
alors après remise au propre, je trouve pour la partie A
circuit 1:
i= (e1-e2)/3R
circuit 2:
i=(i0+e)/2R
Mais pour la partie B aucune idée de comment faire... Je fais lois des noeuds, lois des mailles mais après je ne vois pas comment avancer pour trouver i1 ou i2....
OK pour 1 ;
Nécessairement faux pour 2 : la formule que tu fournie n'est pas homogène. En physique, on ne peut additionner que des grandeurs de même dimension physique ; en particulier pas une tension et une intensité !
Un conseil si tu permets : pense à systématiquement vérifier l'homogénéité des formules littérales que tu obtiens ; cela t'évitera bien des erreurs !
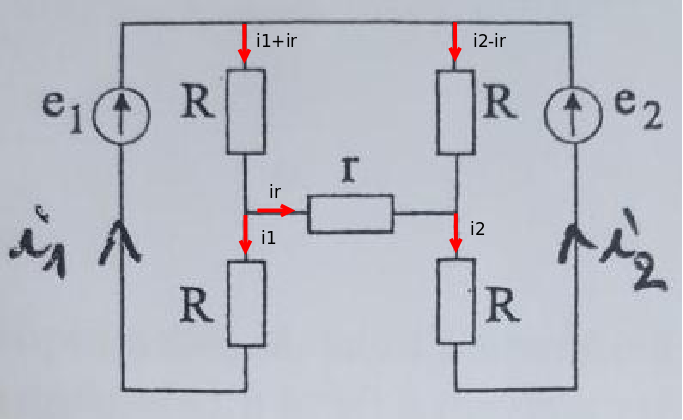
Pour 3 : la loi des nœuds conduit à la répartition des courant que je t'ai fournie sur le schéma. Cela fait intervenir 3 inconnues. Il te faut donc maintenant 3 mailles pour obtenir trois équations indépendantes.
Remarque : procéder ainsi demande un minimum de réflexion mais est préférable à la méthode consistant à introduire autant d'intensités inconnues qu'il a de branches. Bien sûr, cela parait plus facile au premier abord mais cela a l'inconvénient de multiplier le nombre d'inconnues et j'ai remarqué que les étudiants peinent ensuite à éliminer les inconnues inutiles ; ils ont souvent tendance à "tourner en rond". J'ai vu des étudiants qui, après une page de calcul, arrivaient à i1+i2=i1+i2 !
Pour le circuit je comprend vraiment pas... On a un norton parait (sans résistance) qui débite un courant noté I0 (i majuscule), le soucis c'est que ne cours on a vu la transformation thévenin-Norton mais lors de source qui n'était pas idéal (donc avec résistance)
La seule approximation que l'on a fait en cours dans le cas d'un Norton parfait, c'est i=I0.
Donc je vois vraiment pas la simplification ou la transformation où elle se fait...
Pour le troisième circuit, a moins d'erreur, j'obtiens:
(j'ai posé i'=i1+ir et i''=i2-ir)
i1=(e2-2u)/r-(e1-u)/R
i2=(e2-2u)/r+(e2-u)/R (formule qui semble homogène)
Je suis désolé, l'électricité est très obscur pour moi même si j'ai eu l'occasion d'en faire avant
Pour le circuit 2, je t'ai quasiment fourni la réponse hier. Je reprends mon message de 19h28 en le complétant :
Pour le circuit B : voici trois équations pour trois inconnues.
Maille de gauche :
Pour la maille de droite :
Pour la maille centrale :
Je te laisse simplifier et résoudre...
effectivement, j'avais pas fait le lien entre I0 tension du générateur et i intensité du courant...
A moins d'une erreur de calcul ou d'une incompréhension
j'obtiens :
i1= (e1(2R2+rR+1)-e2)/2R2(2R+r)
i2= (e2(2R2+rR-1)+e1)/2R2(2R+r)
Ai-je fais une faute ?? Est ce que c'est le bon résultat ??
En tout les cas, merci pour votre aide
As-tu bien vérifié l'homogénéité de tes expressions ?
r.R-1 : cela n'a pas de sens !
de même : on ne peut additionner e1 au produit de e2 par le carré d'une résistance.
je trouve i1 et i2 en fonction de ir soit:
i1=(e1-Rir)/2R
i2=(e2+Rir)/2R
mais je ne vois pas la suite ni à quoi peut me servir la troisième maille...
Je t'ai fourni dans mon message du 17-11-19 à 15:41 les trois équations correspondant aux trois mailles. Je te laisse refaire le calcul. Sauf erreur de ma part, on obtient :
Compte tenu de la symétrie du circuit, il est rassurant de constater que permutter les indices 1 et 2 de la première expression conduit à la seconde. On pourrait aussi rapidement vérifier la validité de l'expression de ir par application du théorème de Thévenin mais cela n'est pas demandé dans l'exercice.
L'homogénéité des formules est, heureusement, respectée.
Je dois vous avouer que je suis totalement perdu. J'ai pas compris
quel calcul vous permet d'arriver à ce résultat ci...
Si vous pouviez me donner juste les 2-3 premières étapes depuis les équations
que vous m'aviez donné plus haut de manière à ce que je comprenne, ce serait sans refus.
En tous les cas merci beaucoup pour votre aide et le temps précieux que vous m'avez accordé.
Après simplifications, les trois applications de la loi des mailles donnent :
(1)
(2)
(3)
En multipliant les coefficients de (3) par 2 :
(4)
En soustrayant membre à membre : (2) - (1) :
(5)
Par identification de (4) et (5) :
Tu vas constater que ce n'est pas le résultat que je t'ai déjà fourni précédemment... Désolé : dans mon message précédent j'ai commis une étourderie qui revenait à poser r=R... Et oui : les expressions finales précédentes des intensités sont fausses puisqu'elles ne font pas apparaître r. Désolé mais je me rattrape !
Ayant ainsi obtenu ir, on obtiens i1 et i2 en remplaçant ir par son expression dans les équations (1) et (2) :
Ce que j'ai écrit précédemment sur l'influence de la symétrie du circuit reste valide.


 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum