Niveau licence

Electricité - Kirchhoff / Thévenin / Norton

Posté par
nSS 14-11-17 à 22:30

Salut !
J'ai tenté de résoudre avec les mutliples méthodes possibles mais je ne sais pas si je n'arrive en aucun cas à arriver au bout du système ...
Mais c'est surtout le fait qu'il y ait 2 générateur de courant qui me bloque...
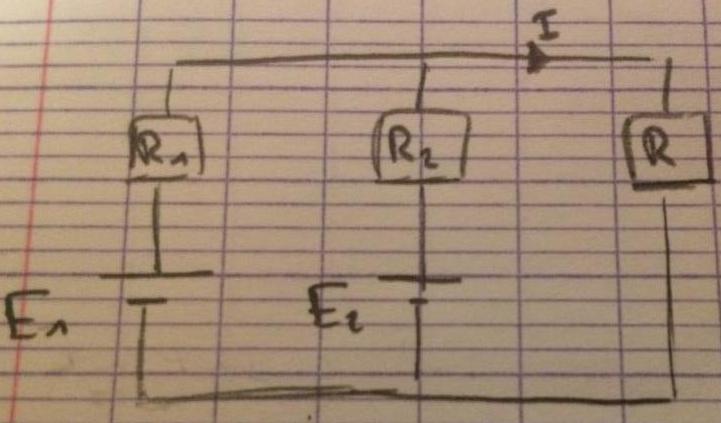
(J'ai mis le schéma en image jointe)

Voici l'énoncé :
Calculer le courant I du circuit ci-contre par 2 méthodes différentes choisies parmi les 3 suivantes :
1) 1ère méthode : Ecrire les lois de Kirchhoff, donner l'expression littérale de I en fonction de E1, E2, R1, R2 et R et calculer sa valeur.

2) 2ème méthode : appliquer le théorème de Thévenin en expliquant bien toutes les étapes de votre raisonnement.
On prendra R=1Ω, R1 = R2 = 2Ω, E1 = 8V, E2 = 4V

3) 3ème méthode : appliquer l'équivalence Thévenin-Norton en remplaçant chaque générateur de tension par le générateur courant équivalent. Refaire le dessin et indiquez sur votre schéma les sens de parcours et les valeurs Icc1, Icc2 débitées par ces générateurs de Norton ainsi que les valeurs de leurs résistances. Simplifiez votre schéma et retrouver la valeur du courant I parcourant la résistance R.

Merci d'avance pour les réponses !

Electricité - Kirchhoff / Thévenin / Norton

Posté par re : Electricité - Kirchhoff / Thévenin / Norton 14-11-17 à 23:03

Bonsoir
Pour un circuit aussi simple, la méthode la plus rapide consiste sans doute à appliquer la loi des nœuds :
I=I₁+I₂
sans appliquer ensuite la loi des mailles mais simplement en remplaçant les intensités par leurs expressions en fonction de la loi d'Ohm :

$\frac{U}{R}=\frac{E_{1}-U}{R_{1}}+\frac{E_{2}-U}{R_{2}}$

$U\left(\frac{1}{R}+\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)=\left(\frac{E_{1}}{R_{1}}+\frac{E_{2}}{R_{2}}\right)$

$U=\frac{\frac{E_{1}}{R_{1}}+\frac{E_{2}}{R_{2}}}{\frac{1}{R}+\frac{1}{R_{1}}+\frac{1}{R_{2}}}$

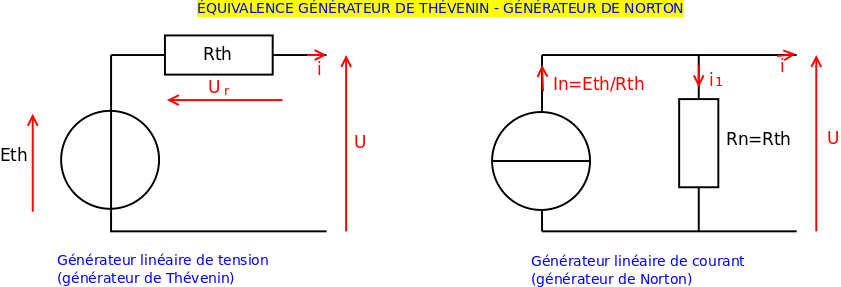
Ayant ainsi la valeur de U, il est facile ensuite de déterminer chaque intensité. Tu peux aussi remplacer chaque générateur linéaire de tension par son générateur linéaire de courant équivalent, regrouper astucieusement les résistances et revenir à un seul générateur de tension alimentant R. Je te laisse réfléchir à cela et proposer une solution. Les schémas ci-dessous pourront peut-être t'aider...

Electricité - Kirchhoff / Thévenin / Norton

Posté par re : Electricité - Kirchhoff / Thévenin / Norton 14-11-17 à 23:44

Pardon, mais j'y ai absolument rien compris...
J'ai trouvé avec ce que j'en sais :
I = I1 + I2
E1 = R1 x I1 + R x I
E2 = R2 x I2 + R x I
Et après ça je n'arrive pas à résoudre le système, je suis tombé sur ça :
(E1/R1) + (E2/R2) = I + ((R x I)/R1) + ((R x I)/R2)

Mais pour l'équivalence Thévenin-Norton, je ne la comprend pas non plus ^^' (Déja que pour Thévenin j'arrive pas à calculer Eth...)

Posté par re : Electricité - Kirchhoff / Thévenin / Norton 15-11-17 à 09:43

J'ai simplement utilisé la loi d'Ohm :

$I=\frac{U}{R}\quad;\quad I_{1}=\frac{E_{1}-U}{R_{1}}\quad;\quad I_{2}=\frac{E_{2}-U}{R_{2}}$
Cette méthode a l'avantage d'avoir directement une équation à une seule inconnue. Ce que tu a fait est bien aussi ; si tu factorises, tu obtiens une expression de I correcte :

$I=\frac{\frac{E_{1}}{R_{1}}+\frac{E_{2}}{R_{2}}}{1+\frac{R}{R_{1}}+\frac{R}{R_{2}}}$
On obtient d'ailleurs cette expression en divisant par R l'expression de U que j'ai obtenue.

Posté par re : Electricité - Kirchhoff / Thévenin / Norton 15-11-17 à 09:46

Remplacer l'ensemble E1 R1 par le générateur de courant équivalent , faire de même pour E2 R2 puis regrouper
...
Je te laisse réfléchir ...

Posté par re : Electricité - Kirchhoff / Thévenin / Norton 15-11-17 à 13:59

Merci beaucoup ! Je viens de comprendre ^^"

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Electricité - Kirchhoff / Thévenin / Norton

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique