Inscription / Connexion Nouveau Sujet
électrcité-circuit complexe
Bonsoir, j'ai un dm à faire et je bloque sur une question, voici l'énoncé :
Montrer que, en posant 
=L/R l'équation différentielle vérifiée par s peut se mettre sous la forme:
3d2s/dt2 + 4ds/dt + 1/2
J'ai commencé comme ceci:
Loi des noeuds:
i=i1 + i2
i=i4 + i3
Loi des mailles:
E=Ri + Ldi4/dt + Ri2
0=Ldi4/dt -Ri3
0=Ri2 - Ldi1/dt
0=Ldi4/dt -Ri3[/bleu]
Ldi4/dt -Ri + Ri4=0
Ri=Ri4 + Ldi4/dt
E=Ri + Ldi4/dt + Ri2
E= Ri + Ldi4/dt +Ri -Ri1
E= 2RI + Ldi4/dt -Ri1
E= 2(Ri4 + Ldi4/dt) + Ldi4/dt - Ri1
E= 2Ri4 + 3Ldi4/dt -Ri1
Voilà, je bloque ici, je n'arrive pas à exprimer "-Ri1" en fonction de s(t). ( s(t)= Ldi4/dt)
Ensuite, en dérivant, on obtient:
3Ld2i4/dt2 + 2Rdi4/dT -Rdi1/dt=0
3 Ld2i4/dt2 + (2R/L)x(Ldi4/dt) - Rdi1/dt=0
Je bloque donc ici. Merci beaucoup d'avoir pris le temps de me lire, et de m'aider, bonne soirée ! 
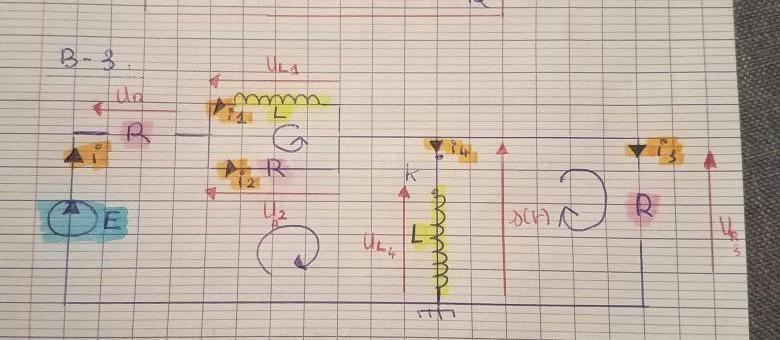
Bonsoir
Il existe une méthode très simple mais elle n'est pas au programme de toutes les filières. On traite le problème en régime sinusoïdal en supposant que la fém est sinusoïdale et en raisonnant sur les complexes. L'étude est très simple en remplaçant les associations (L//R) par leur impédance complexe. On tombe sur un simple diviseur de tension.
On revient ensuite au domaine temporel en faisant correspondre à
la dérivée nième de s(t) par rapport à t.
On évite ainsi les calculs fastidieux correspondant à l'application de la loi des nœuds et des mailles.
L'équation différentielle que tu fournis n'est pas complète. Cependant, sous réserve de deux inductances identiques et de trois résistances identiques, l'équation différentielle est beaucoup plus simple que celle que tu proposes. Es-tu bien sûr que l'équation, même incomplète, que tu proposes correspond bien à ce circuit ?
Vanoise, merci d'avoir répondu aussi vite, nous n'avons pas encore parlé de cette méthode en cours, mais c'est dans mon programme et on ne va pas tarder à l'aborder. Je ne sais donc pas encore comment m'y prendre et je doute que ma prof attende de nous une telle méthode de résolution. 
vanoise Oui pardon en effet, j'ai oublié une partie de l'équation en la retapant, la voici :
3 d2s/ dt2 + 4ds/dt + s/2=0
Effectivement, cette méthode n'est pas demandée dès le début de sup.
J'ai tout de même un problème avec cet énoncé. La méthode directe et la méthode des complexes conduisent à un même résultat beaucoup plus simple que celui proposé :
Je ne suis pas infaillible : faute d'avoir un labo d'électronique chez moi, j'ai réalisé des simulations informatiques qui conduisent aussi à ce résultat simple. Erreur d'énoncé ? Cette formule s'applique peut-être à un autre montage ???
La démonstration est très simple si on remarque que les deux associations (R//L) sont identiques et associées en série. On peut donc poser simplement :
u2(t) = s(t) 
t
La loi d'addition des tension conduit alors à :
donc
On dérive tous les termes par t pour se débarrasser de la primitive :
Aussi simple que cela ! Un conseil : quand cela est possible, évite la méthode dite « des nœuds et des mailles » ; certes, elle s'écrit simplement mais conduit ensuite à des calculs souvent inextricables...
Annuler
connectez vous