Pourquoi ne pas faire un dessin?

Pythagore te donne la distance entre le passant et l'ambulance.

L'ambulance se situe à 1m derrièr elui.

On en déduit que .

On projette ensuite la vitesse sur la droite reliant le passant à l'ambulance afin d'en déduire la vitesse radiale.



Ensuite, il ne reste qu'à utiliser la formule précédente.

je peux faire un dessin et puis vous pourriez le corriger si cest faux?

bonsoir , bonsoir


voila, j'ai fait un dessin de l'enonce , mais je ne comprends toujours pas comment on on projecte pour calculer coss .
Je voudrais aussi savoir pour la premiere figure, si elle marchait avec vs et vr dirige vers la gauche


Merci

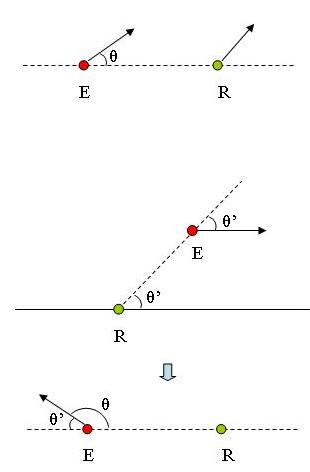
Dans ton second dessin, l'angle représente l'angle situé au niveau du point R de ton triangle rectangle.

C'est aussi l'angle entre la direction de l'ambulance et la ligne de propagation reliant l'émetteur au récepteur.

Si tu as une formule toute faite dans ton cours, alors oui, elle est valable quel que soit l'angle , que celui-ci soit supérieur à ou non.

seulement, la situation est légèrement différente sur ton second schéma. A toi d'en tenir compte dans ton calcul.

justement , je voulais savoir comment projecter pour etre dans les conditions du  1er schema /

" Dans ton second dessin, l'angle \theta représente l'angle situé au niveau du point R de ton triangle rectangle.

C'est aussi l'angle entre la direction de l'ambulance et la ligne de propagation reliant l'émetteur au récepteur.
"



Ce que tu parles c'est le theta R , or on veut exprimer avec le theta s car dans l'énonce on me dit que le passant ne bouge , il ya juste l'ambulance qui a vitesse donc cos(theta R ) = 0

Je voulais savoir aussi si costhetaS ( SR , d ) = costhetaR

MErci

Désolé rectification  cos ( SR , d ) = cosS

Non, l'angle que je t'indique  est celui qui est pertinent. D'ailleurs, tu le dis toi-même, la vitesse du passant est nulle. Comment pourrait-on déterminer un angle entre une droite et un vecteur inexistant? Ce que tu appelles n'est pas défini ici. La réponse a ta dernière question est donc non.

Oublie donc ton premier schéma un instant et prends un peu de recul (ou alors tâche de l'adapter au problème de façon convenable).

Je pense que tu ne saisis pas bien le sens de l'effet Doppler. Cet effet est lié à la variation de distance entre un émetteur et un récepteur. C'est pourquoi on projette les vitesses du récepteur et de l'émetteur sur l'axe les reliant. Les composantes de ces vitesses selon cet axe contribuent toutes les deux à l'éloignement ou au rapprochement de l'émetteur et du récepteur.

D'après le schéma, il est évident que l'angle recherché est aussi l'angle formée en R par l'horizontale et la ligne reliant l'ambulance au passant .

Pour te placer dans les conditions de ton premier schéma, il suffit de prendre, ou est l'angle que je t'ai indiqué.

Si tu visualises bien les choses (et notamment comment les vitesses contribuent à l'effet Doppler) tu ne devrais pas avoir de problème.

Je pense que j'ai vraiment un probleme pour la transposition , je ne vraiment à voir que s = - pour etre dans les conditions du 1 . De plus je ne vois pas comment on peut exprimer l et d dans ces conditions car on m'a dit qu'il faut avoir qu'il faut avoir coss = L/ L²+d²

L et d sont des grandeurs propres au problème.

Elles n'ont rien à voir avec ton schéma général.

Effectue le calcul avec la valeur que l'on t'a "donnée" et dis-moi ce que tu trouves pour la valeur de la fréquence.

388 HZ mais j'aimerais bien savoir comment on trouve cette formule et le lien avec s = -

Détaille ton calcul.

Si tu arrives au bon résultat (et a priori c'est le cas), c'est qu'à un moment donné tu as bien pris en compte les différences entre ton premier et ton second schéma.

non , j'ai justement applique la formule qu'on ma donné betement .

Tout le calcul reside dans costheta s , une fois qu'on a trouve alors le calcul est fini .

Il reste encore a calculer la fréquence et par conséquent à prendre en compte correctement la vitesse de l'émetteur, non?

Remarque que . C'est toute la différence entre un émetteur qui se rapproche et un émetteur qui s'éloigne.

ah ok je vois mieux alors , donc ce cas comme on sait que coss = -cos = L/L²+d² .

Mais je ne comprends toujours pas pour la transposition en fonction du 1er schema pour arriver a s = -

Manifestement, tu utilises des formules toutes faites... Dans ce cas, tu es bien obligé de respecter les conventions sur lesquelles elles reposent.

Sur ton premier schéma, on mesure l'angle à partir de la ligne reliant l'émetteur et le récepteur, dans le sens trigonométrique. Sur le second, tu mesures l'angle à partir de la même ligne, mais dans le sens anti-trigo. Il faut bien prendre cette différence en compte. Il suffit de comparer les deux schémas pour voir que les deux façons de mesurer sont complémentaires et que l'un des angles correspond à pi moins l'autre.

Mais on peut aussi, sans risque de se tromper, ignorer complètement les histoires de signe dans un premier temps, à partir du moment où la valeur de la vitesse est correcte en valeur absolue. En effet, il suffit ensuite de regarder le schéma pour déterminer si le récepteur s'éloigne (signe -) ou se rapproche (signe +). C'est l'avantage de la physique, on peut toujours se reposer sur ce genre de considérations pratiques.

Vous n'auriez pas une figure ou dessin, car j'ai vraiment du mal à saisir . En reprenant votre explication , le correspond au r ( meme si il n'existe pas dans cet exemple )


merci

En reprenant mon explication, l'angle calculé ne correspond sûrement pas à un angle qui n'existe pas...

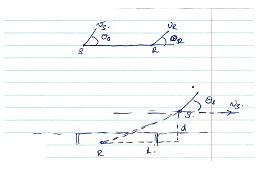
Je joins le schéma que tu aurais pu/dû faire toi-même.

Dans le problème de l'ambulance et du passant, on calcule facilement à l'aide de quelques observations géométriques de base un angle . Si on le compare à ton schéma général, on se rend compte que ce n'est pas l'angle que l'on utilise pour le calcul de la fréquence Doppler.

En revanche on voit (immédiatement!) que puisque ces angles sont supplémentaires.

Et, encore une fois, puisque , la différence ne tient au final qu'à un signe que l'on est en mesure de corriger en décidant si l'émetteur se rapproche ou s'éloigne. Mais bien sûr, cela nécessite de comprendre un minimum le problème...

MERCI !