Inscription / Connexion Nouveau Sujet
Dynamique non galiléenne
Bonsoir,
J'arrive pas à comprendre une question d'un exercice ,merci de m'aider.
Donc voilà l'enoncé:
On etudie le mouvement d'une balle de fusil tirée horizontalement dans la direction du nord puis du point M d'altitude h=2m.
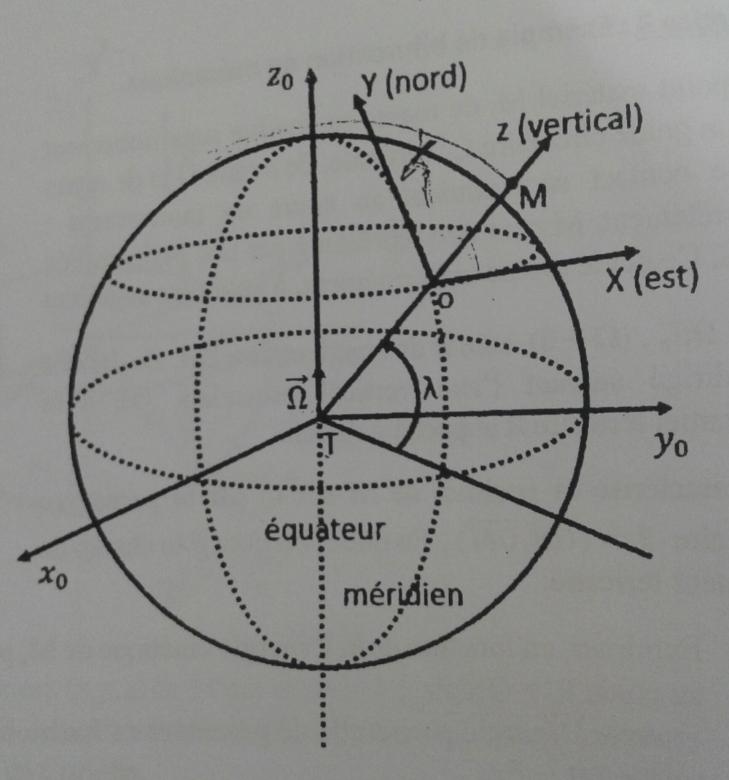
R=R(o,x,y,z): référentiel terrestre.
La question: déterminer la position de l'impact de la balle en considérant que le referentiel terrestre R est galileen.
Bonsoir
Le fait de faire intervenir la latitude et de préciser les orientations des axes (OX) et (OY) donne l'impression que ce problème est une variante de la classique étude de la "déviation vers l'est" lors d'une chute libre mais l'énoncé précise que le repère terrestre doit être considéré comme galiléen...
Dans ces conditions, en négligeant les frottements de l'air, tu tombes sur un banal exercice niveau terminale sur les trajectoires paraboliques.
La notion de pseudo force d'inertie de Coriolis a-t-elle été étudiée déjà en cours ?
Salut,
Comme le référentiel doit être considéré comme galiléen (donc pas de Coriolis) ... et si on ne doit pas tenir compte des frottements (???)
Ce que je vois comme différence possible avec une simple trajectoire parabolique est qu'on doit peut-être tenir compte de la sphéricité de la Terre.
La Force agissant sur le projectile est "verticale" ... mais cette verticale change de direction en cours de trajectoire par la sphéricité de la Terre.
Ce qui est "peut-être" attendu est de trouver le point d'impact en "oubliant" les effets du à la nature non parfaitement inertielle du référentiel et les frottements ... mais en tenant compte de la courbure de la Terre.
Supposition évidemment et bien conscient que l'effet de la sphéricité de la Terre aura, dans beaucoup de cas un effet bien plus petit que les autres effets négligés (rotation de la Terre, frottement ...).
bien conscient que l'effet de la sphéricité de la Terre aura, dans beaucoup de cas un effet bien plus petit que les autres effets négligés (rotation de la Terre, frottement ...).
Tout à fait d'accord : j'aurais même tendance à écrire, puisqu'il s'agit d'une simple balle de fusil : "dans tous les cas"...
Il est explicitement précisé que le repère terrestre doit être considéré comme galiléen mais la figure représente un vecteur rotation instantané non nul. Tout cela est contradictoire...
Bonsoir
Le fait de faire intervenir la latitude et de préciser les orientations des axes (OX) et (OY) donne l'impression que ce problème est une variante de la classique étude de la "déviation vers l'est" lors d'une chute libre mais l'énoncé précise que le repère terrestre doit être considéré comme galiléen...
Dans ces conditions, en négligeant les frottements de l'air, tu tombes sur un banal exercice niveau terminale sur les trajectoires paraboliques.
La notion de pseudo force d'inertie de Coriolis a-t-elle été étudiée déjà en cours ?
On ne parle pas de force de coriolis tant qu'on n'a pas tenir compte de la rotation uniforme de la terre autour de l'axe polaire(c'est dans la suite de l'exercice qu'on tiendra compte de cela)
Ce que j'ai pas compris est l'expression 'position de l'impact'.
Bonsoir
Le fait de faire intervenir la latitude et de préciser les orientations des axes (OX) et (OY) donne l'impression que ce problème est une variante de la classique étude de la "déviation vers l'est" lors d'une chute libre mais l'énoncé précise que le repère terrestre doit être considéré comme galiléen...
Dans ces conditions, en négligeant les frottements de l'air, tu tombes sur un banal exercice niveau terminale sur les trajectoires paraboliques.
La notion de pseudo force d'inertie de Coriolis a-t-elle été étudiée déjà en cours ?
On ne parle pas de force de coriolis tant qu'on n'a pas tenu compte de la rotation uniforme de la terre autour de l'axe polaire(c'est dans la suite de l'exercice qu'on tiendra compte de cela)
Ce que j'ai pas compris est l'expression 'position de l'impact'.
Peut-être faut-il commencer avec ce que j'ai écrit (négliger les effet de la rotation de la Terre et les frottements et ne tenir compte que de la sphéricité de la Terre).
On bien ne pas tenir compte de la sphéricité de la Terre ?
Va savoir. L'énoncé est mal foutu pour se faire une opinion.
Et ce sont les questions qui suivent (non déjà mentionnées ici) qui demanderont l'influence de la rotation de la Terre sur le point d'impact.
Quant aux frottements dans l'air, devra-ton au non en parler ?
Leurs effets sont cependant non négligeables pour un tir de fusil.
No se



