Bonjour
Il faut commencer par faire un schéma clair où sont représentées les différentes actions exercées sur le disque par le milieu extérieur. Il faut ensuite appliquer les théorèmes généraux de la mécanique...
Je te laisse réfléchir et proposer une solution... Expose au besoin ce qui te bloque.

M., Voilà ce que j'ai fait mais le soucis c'est que je n'ai pas répondu à la question qui est celle de déterminer la durée. Et je ne sais pas si l'énergie cinétique calculée au niveau du TEC est bien faite.

** image supprimée **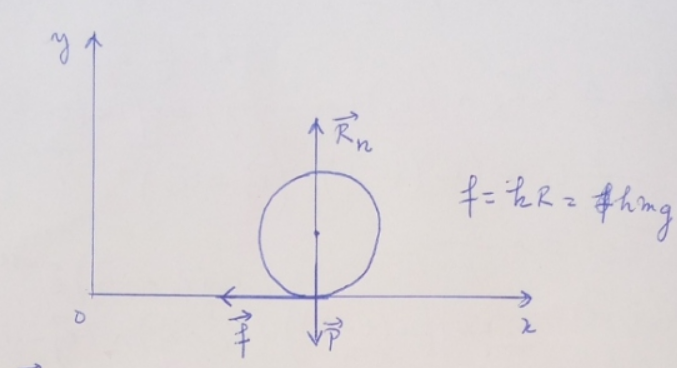


_{* mmalou > Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier tes recherches sur le forum Nerf *}

Bonjour
il est urgent de lire ce qui est autorisé ou pas

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Ta figure n'est pas claire. Il s'agit de celle qui correspondrait à un roulement sans glissement à vitesse constante car la force que tu sembles faire intervenir ne travaille pas.

Tu écris : f= h.R ; que désigne f ? Tel que tu définis f, il s'agit de l'aire d'une surface, et tu représentes un vecteur force !  As-tu bien compris ce que désigne "h" dans ton énoncé ?
Une fois tout cela tiré au clair, les théorèmes généraux de la mécanique vont te permettre de déterminer l'accélération de C et l'accélération angulaire de la roue. Tu pourras en déduire la durée du mouvement avant l'arrêt.

h étant un coefficient de frottement, alors la force de frottement liée à h est f=hR_n où R_n est la réaction normale du plan horizontal et de ce fait R_n=mg d'où ce que j'ai écrit...
Je pense que cette force travaille car c'est grâce à elle que le solide s'arrêtera au bout d'un moment. Étant une force de frottement, elle est dirigée par définition dans la direction du mouvement en sens contraire. W(f)=-fd.

A ce que tu as écris dans ton premier message, h est une distance, probablement celle notée b_v sur ce document :

Ok monsieur. Je sais maintenant ce qu'est exactement le coefficient de  frottement de roulement. Je vous remercie.

Mais malheureusement ça ne m'a pas permis d'avancer dans la résolution de l'exercice ou du moins je ne vois pas comment me servir de ces éléments.

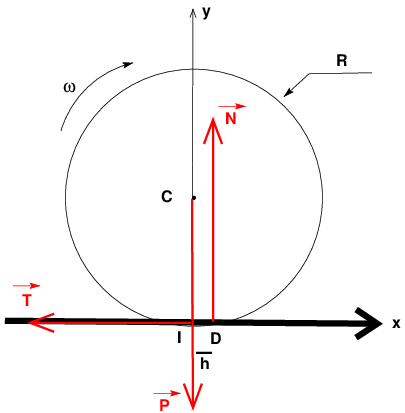
Tu peux t'aider du schéma ci-dessous. Le contact avec le sol n'est pas ponctuel en I comme cela se modélise de façon simplifiée. La roue se déforme localement de façon à donner une surface de contact sur laquelle la pression exercée par le sol sur la roue n'est pas uniforme ; elle est plus élevée sur la partie avant de la surface. On rends compte de tout cela en considérant que le sol exerce sur la roue deux forces :
La réaction tangentielle   appliquée en I comme en absence de frottement de roulement et la réaction normale exercée non pas en I mais en D avec h : distance ID.
Il te reste maintenant à appliquer le théorème du moment dynamique en C dans le repère (Cxy). C'est là qu'intervient le théorème de König : il affirme que le théorème du moment cinétique s'applique en C dans le repère barycentrique (Cxy) même si ce repère n'est pas galiléen... Il faut aussi utiliser le théorème du centre d'inertie dans le repère galiléen lié à la terre.

Ok monsieur. Si j'ai bien compris voilà :
En appliquant cette formule entre l'instant où le solide a une vitesse de rotation w_o et l'instant où il s'arrête, on a :
Or
Donc, avec N=mg et J=mR²/2.
Ainsi, .

Monsieur c'est ça ?

Non : La projection du théorème du moment cinétique en G dans le repère barycentrique donne :



La projection de la relation fondamentale de la dynamique (théorème du centre d'inertie) donne :





Je te laisse continuer

Ah d'accord monsieur. Je pensais que T=Nh. Juste une dernière question au niveau de la projection du moment cinétique, lorsque je calcule et je me retrouve avec un moins devant TR..

Je vous remercie infiniment pour cette aide.

Une relation de la forme T=N.h supposerait h : coefficient sans dimension ; or : h a la dimension physique d'une distance. Attention : la force ne travaille pas et n'influence pas directement l'accélération ; elle permet à la roue de rouler plutôt que de glisser. Elle existe même en absence de frottement de roulement.
Pour les signes : les lettres T,N et P désigne les normes des vecteurs forces. Cela est cohérent avec le fait que le mouvement est retardé : la vitesse angulaire décroit : sa dérivée par rapport au temps est négative.

Désolé monsieur. Je me suis mal exprimé. En fait je pense que ça devrait plus être -TR au lieu de +TR.

Regarde bien la figure : la force tend à faire tourner la roue dans le sens positif choisi ; son moment par rapport à l'axe instantané de rotation (C,z) est donc positif, d'où le "+T.R" dans la formule...

Mr mais pourquoi en appliquant la définition du moment par rapport à C CI×T le moins apparaît ?  C'est ça qui me semble incompréhensif..

Quand, comme ici, la direction du vecteur force appartient à un plan perpendiculaire à l'axe de rotation, tu peux calculer simplement le moment de la force en écrivant que ce moment vaut où T est la norme du vecteur force, ”d” la longueur du bras de levier, ici : d=R et un signe qui obéit aux règles suivante :

1° : un signe + si la force tend à faire tourner le solide dans le sens positif choisi ;

2° : un signe - si la force tends à faire tourner le solide dans le sens négatif choisi.
Compte tenu du sens positif indiqué sur la figure, le moment est ici positif.

Autre méthode un peu plus compliquée : tu calcules le moment vectoriel de la force en C : et tu projettes ensuite sur l'axe de rotation. Compte tenu du sens de rotation choisi, l'axe (C,z) doit être orienté vers l'arrière de la figure (règle du tire-bouchon de Maxwell).
Exemples ici :

Ah oui je vois maintenant où je faisais erreur.