Inscription / Connexion Nouveau Sujet
Dynamique des points
Bonjour, un coup de main s'ils vous plaît.
Exercice
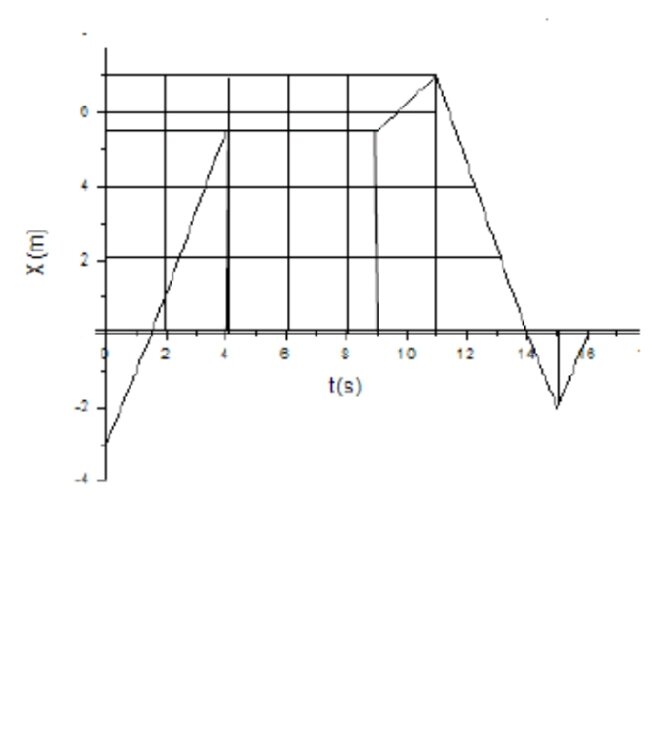
La position d'un mobile en fonction du temps est indiqué sur la position ci-dessous.Indiquer:
1)En quel endroit le mouvement de fait dans la direction des X positif ou négatif ?
2)A quel instant le mouvement est retardée ou accélérer ?
3)A quel instant le corps passe par l'origine?
4)A quel instant la vitesse est nulle ?
5) Faire un graphique de la vitesse et de l'accélération en fonction du temps
6) Estimé d'après le graphique la vitesse moyenne sur les intervalles de temps:
1s<t<1,8s ; 1s<t<2,2s ;1s<t<3s
1) je cherche les équations horaires d'abord
Sur t€[0,4s]
x(t)=V(t-t0)+X0
or V=(x1-X0)/t1-t0=(5,5-3)/4-0=2,13m/s
X0=-3m
X1(t)=2,13t-3
-Pour t€[4, 9s]
X2(t)=5,5
-Pour t€[9,11s]
X3(t)=0,75t-1,25
- Pour t€[11, 15s]
X4(t)=-2,25t+31,75
- Pour t€[15, 16s]
X5(t)=-2t+28
1) je me demande si équations horaires sont nécessaires pour répondre à la 1ere question ou bien répondre seulement à partir du graphique?
Bonjour,
Les équations horaires ne sont pas utiles : les questions portent sur la vitesse et l'accélération, il faut donc calculer quoi ?
Remarque : à mon avis, la première question est la question 5 !
Oui certainement !
Du coup je ne sais pas comment répondre pour la 1ere question
Toutefois Je sais que les x sont positifs pour t€[1,5;14s] et les x sont négatif pour t€[0; 1,5s] et [14,16s]
La question 1 concerne la direction du mouvement donc la vitesse et pas la position.
D'où l'intérêt de faire en premier la question 5.
D'accord mais je ne sais comment commencer , pourrez vous me déterminer un point de coordonnées (t ,V) comme ça je vais essayer de trouver les autres points et les placer dans le graphique
La vitesse c'est la variation de la position en fonction du temps. Donc la dérivée de x par rapport au temps :dx/dt
C'est bien cela.
Donc vous pouvez répondre à la question 1.
Pour 2, même question que précédemment, mais à l'ordre suivant pour l'accélération.
Pour 3, lecture du graphe
Pour 4 idem 1
Ok donc pour 1 j'aurais;
1) V1=(X1-X2)/(t1-t0)
=(5,5+3)/(4-0)=8,5/4= 2,13 m/s( sens des X positif)
V2=0 m/s
V3=(7-5,5)/(11-7)= 1,5/2=0,75m/s( sens des X positif)
V4=(-2-7)/(15-11)=-9/4=- 2,25m/s( sens des X négatif)
V5=(0-2)/(16-15)=-2m/s (Sens des X négatif)
Bonjour,
2) je cherche les accélérations :
a1=(V2-V1)/(t2'-t1')=(0-2,13)/(9-0)
=0,24m/s²( mouvement accélérer pour t€[0,9s] )
a2=(V3-V2)/(t3'-t2'')=(0,75-0)/(11-4)
=0,11m/s²( mouvement accélérer pour t€[4, 11s])
a3=(-,2,25-0,75)/(15-9)= -0,5m/s²
(Mouvement retardée pour t€[9,15s] )
a4=(2+2,25)/(16-11)= 0,85m/s²
( mouvement accélérer pour t€[11, 16s])
Vos calculs ne sont pas faux, mais ce sont des accélérations moyennes qui n'on pas grand sens.
L'accélération est la dérivée de la vitesse et comme celle-ci est constante par morceaux, l'accélération est nulle, sauf quand on change de vitesse (passage de V1 à V2, V2 à V3 ...), et comme la modification est instantanée à l'échelle du graphique, elle n'est pas calculable.
Par exemple à t=4 la vitesse passe de 2 à 0, donc ?
J'ai indiqué "comme la modification est instantanée à l'échelle du graphique, (l'accélération) n'est pas calculable. "
Il s'agit juste de trouver son signe, si la vitesse (positive) diminue, elle est négative, on freine.
Plutôt 4, 9, 11 et 15 (rupture de pente) et ceci avec une accélération algébrique.
Il faut maintenant savoir dans quel cas il y accélération (au sens non algébrique) et freinage.
Pour t=4 on passe de 2 à 0 donc on freine (jusqu'à s'arrêter)
Pour t=9 on passe de 0 à 0,75 donc on accélère (on démarre)
Pour t=11 on passe de 0,75 à -2, donc il a d'abord fallu freiner pour s'arrêter et accélérer pour repartir dans l'autre sens.
Pour t=15 on passe de -2 à 2, donc il a d'abord fallu freiner pour s'arrêter et accélérer pour repartir dans l'autre sens.


