Inscription / Connexion Nouveau Sujet
Dynamique des fluides
Bonjour à tous,
Voici mon exercice :
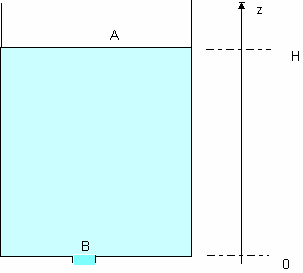
On utilise en travaux pratiques une cuve verticale (voir schéma ci-dessous) remplie d'eau ; on supposera que le niveau A dans la cuve est constant. Le fluide s'écoule par un trou de diamètre D situé dans le fond de la cuve. L'eau sera considérée comme un fluide parfait incompressible.
Appliquer la relation de Bernoulli entre les points A et B et déterminer l'expression littérale de la vitesse VB au niveau du trou.
Dois je obligatoirement utiliser le théorème de Bernoulli pour déterminer vB ?? (Je l'utilise en effet une première fois pour déterminer la pression pB)
Si oui est ce que utiliser (1/2)
VB2 + gzB + pB = cste est correct ?
(2pB/
15 m.s-1 .....
Salut,
Je passe par un bilan d'énergie (et donc Bernouilli), en supposant que la vitesse d'écoulement àla surface de l'eau du bac est négligeable par rapport à la vitesse d'écoulement en sortie du bac :
v²/2 + gz + P/Rho = constante.
vA²/2 + g.zA + PA/Rho = vB²/2 + g.zP + PB/Rho
Comme la section du récipient est beaucoup plus grande en A que en B, on peut négliger VA devant VB (donc considérer VA comme quasi nulle) --->
g.zA + PA/Rho = vB²/2 + g.zP + PB/Rho
VB²/2 = g(zA-zB) + (PA-PB)/rho
PA étant la pression de la surface libre du liquide (donc PA = P atmosphérique)
PB étant la pression au niveau du jet libre (donc coté extérieur du bas du réservoir) --> (donc PB = P atmosphérique)
On a donc PA - PB = 0.
Il reste alors : VB²/2 = g(zA-zB) = g.H
vB² = 2g.H
Merci beaucoup pour ta réponse !
Mais je voudrais savoir, la pression au point B ne rentre pas en compte ??
Pour le fun:
On peut faire autrement (même si on ne voit pas souvent (jamais ?) fait ainsi).
Delta pression des 2 cotés du trou : Delta P = Rho * g * H (pression hydrostatique)
Supposons un tube de sortie de longueur L :
La force exercée sur la masse d'eau dans le tube de sortie est F = Delta P * S (avec S la section du tube (donc du trou))
La masse d'eau dans le tube est m = Rho * S * L
On calcule l'accélération de l'eau dans le tube par : F = m.a
Delta P * S = Rho * S * L * a
Rho.g.H * S = Rho * S * L * a
a = g.H/L
La vitesse de l'eau à la sortie du tube est : v = a * t
avec L = at²/2
t = Racinecarrée(2L/a)
v = gH/L * Racinecarrée(2L/(gH/L)) = Racinecarrée(2L*gH/L)
v = Racinecarrée(2gH)
indépendant de la longueur L du tube de sortie ... et donc aussi avec L --> 0, donc un simple trou (sans tube)
Cette méthode néglige les pertes de charge dans le tube de sortie ... ce qui n'influence pas le résultat si on considère que L --> 0.
-----
Je ne conseille pas de le faire ainsi, cela ne serait probablement pas accepté par le prof, bien que ...
Annuler
connectez vous