Inscription / Connexion Nouveau Sujet
dynamique des fluides
Bonjour, on me demande de montre en considérant un écoulement stationnaire et en utilisant l'équation de continuité que tout le flux qui rentre à travers la surface entouré par
doit sortir à travers
entouré par
.
J'ai comme indication d'utiliser le théorème de la divergence.
Tout ce que je peux dire ce que par l'équation de continuité, on a que . Ainsi, par le théorème de la divergence,
Le signe - devant la première intégrale de la dernière égalité vient du fait que et
sont de signe opposé. De plus comme
, on a que
, la deuxième intégrale est donc nul, ce qui me donne au finale
, ce qui me fait arriver à
ce qui est bien sûr faux et je ne vois pas où est mon erreur.
Merci pour votre aide 
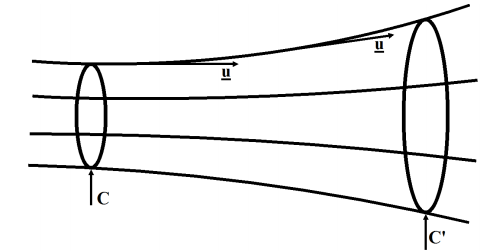
Autre question, dans le cas d'un écoulement quelconque (non nécessairement stationnaire), comment justifier que les ligne de courant ne se coupe jamais ? J'aurais envie de dire que si elle se croisaient, le fluide aurait deux vecteur vitesse différente à un même endroit ce qui n'est pas possible... mais ça me parait un peu mince comme explication.
Merci,

 udS sont égales, mais qui dit que
udS sont égales, mais qui dit que 
