Inscription / Connexion Nouveau Sujet
Dynamique
Bonjour je bloque sur la 1ère question de ce sujet
Un morceau de glace G, de masse initiale M, descend d'un plan incliné d'un angle alpha par rapport à l'horizontale, avec une vitesse initiale vo. Par suite de la fusion G perd une masse μ par unité de temps (μ = cste). Les force de frottements,sont à chaque instant, proportionnelles à la racine carrée de la masse de G, avec un coefficient de proportionnalité k.
1- Déterminer l'équation différentielle qui permet de déterminer la vitesse de G à l'instant t.
Je pense qu'il faut, comme il s'agit d'un système à masse variable appliquer la relation F= dp/dt à p(t) et p(t+dt) mais je n'arrive pas à visualiser comment aboutir sur une vitesse. Merci à vous
Bonjour,
Que vaut en fct de m et
 ?
?
Et ici, en projection sur la ligne de plus grande pente, p = ...
Donc dp/dt = ...
vecteur p = m*vecteur v
Quand on projette p sur la ligne de plus grande pente p = m*v*sin(α)
donc
dp/dt= d(m*v*sin(α ))/dt= v*sin(α )*dm/dt + m*sin(α )*dv/dt + m*v*d(sin(α )/dt
= vsin(α )μ + msin( α )a + mvcos(α )
?
Quand on projette p sur la ligne de plus grande pente p = m*v*sin

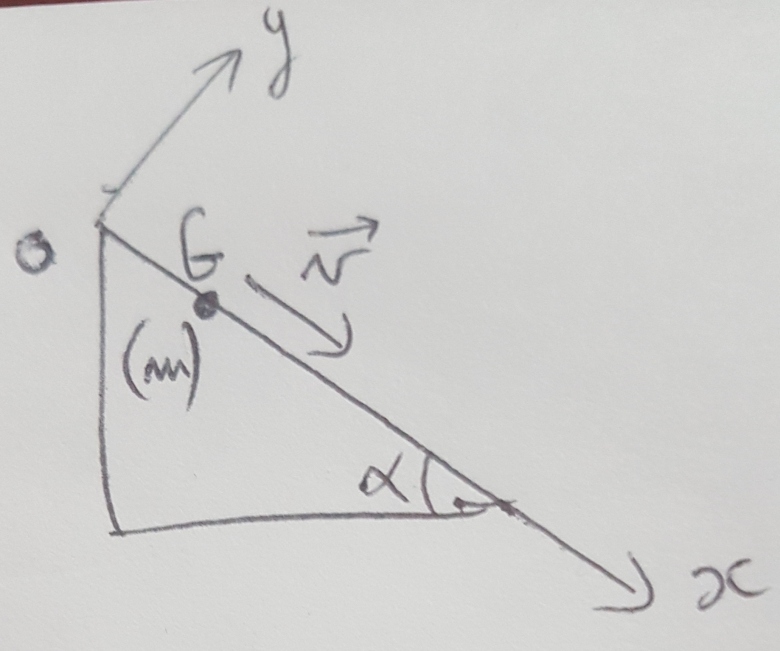
Non, il faut faire un dessin et se placer dans (O,x,y) de façon à ce que le mvt se fasse selon (O,x)