Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Doublet de lentilles\ Optique géométrique

Posté par
tintin22 15-03-22 à 17:17

Bonjour j'ai quelque que problème avec mon exercice, pouvez vous m'aider s'il vous plaît ?
L'exercice en question repose sur un doublet de lentilles.

On considère une lentille mince convergente L_1, de centre optique O_1, de distance focale
f '_1 = 30 cm. On éclaire un petit objet réel AB situé à 50 cm de cette lentille. Son image à travers
L_1 sera notée A_1B_1.

1. a. Donner l'expression de la relation de conjugaison d'une lentille mince dans l'air ainsi que
celle du grandissement.

1. b. Calculer la position \overline{O_1A_1}
̅̅̅̅̅̅̅ de l'image A_1B_1 de AB, donnée par la lentille L_1. Calculer le
grandissement \gamma_1. Quelle est la nature de l'image A_1B_1 (réelle ou virtuelle) ? Renversée/droite ?
Rétrécie/agrandie ?

2. On place une seconde lentille L_2 à 25 cm de L_1 (cf figure 2). La lentille L_2 est également
convergente de centre optique O_2 et de distance focale f '_2 = 50 cm. On notera A'B' l'image de
A_1B_1 par la lentille L_2. Ainsi A'B' est l'image finale de l'objet AB par le doublet de lentilles
formée par L_1 et L_2.

2. a. Calculer la valeur algébrique \overline{F_2F'_1}
̅̅̅̅̅̅̅ à l'aide de la relation de Chasles.

2. b. Calculer la valeur algébrique \overline{O_2A_1}
̅̅̅̅̅̅̅ à l'aide de la relation de Chasles.

2. c. Puisque A_1 et A' sont conjugués par L_2, calculer la position \overline{O_2A'}
̅̅̅̅̅̅ de l'image A'B' donnée
par le doublet de lentilles. Calculer le grandissement \gamma_2 de la seconde lentille L_2 puis le
grandissement \gamma de l'ensemble du doublet. L'image finale est-elle droite ou renversée ?

2. d. Calculer la position \overline{O_1F} du foyer principal objet F de l'ensemble du doublet.

2. d. Calculer la position \overline{O_2F'} du foyer principal image F' de l'ensemble du doublet.

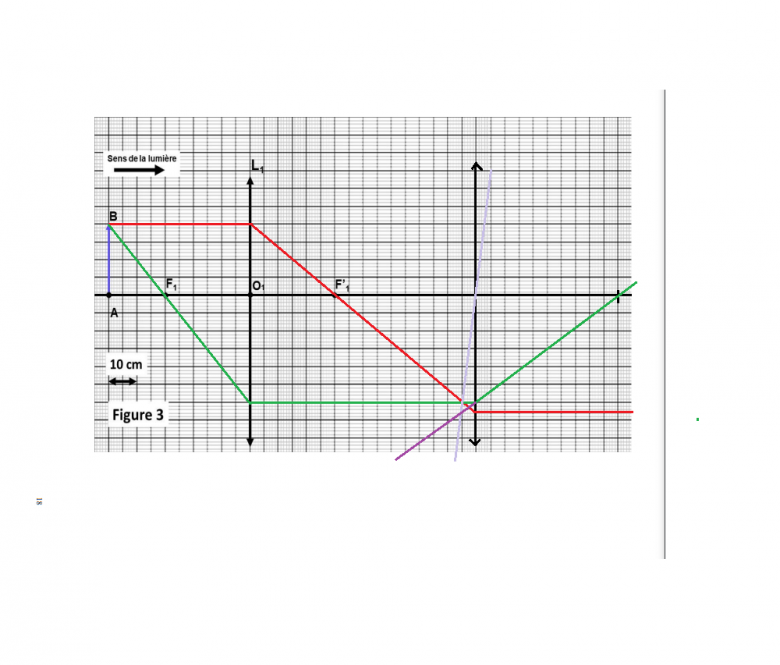
3. On déplace la lentille L_2 de 55 cm vers la droite.

3. a. Placer cette lentille L_2 ainsi que ses foyers F_2 et F'_2 sur la figure 3 (on notera que l'échelle a
changé). Que remarquez-vous ?

3. b. Dans cette configuration particulière, le système est dit afocal. A partir de la figure 3,
construire l'image finale A'B' de l'objet AB. Pour cela on construira la marche d'un rayon
incident parallèle à l'axe optique et d'un rayon incident passant par F_1 ; ces deux rayons
incidents passant bien sûr également par B.

3. c. L'image finale est-elle réelle ou virtuelle ? L'image finale est-elle droite ou renversée ?

Ce que j'ai déjà fais :

1a) Relation de conjugaison :\frac{1}{\overline{OA}} = \frac{1}{\overline{OA'}} -  \frac{1}{\overline{OF'}}

grandissement : \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{OA'}}{\overline{OA}}

b) \frac{1}{\overline{O_1A}} = \frac{1}{\overline{O_1A_1}} -  \frac{1}{\overline{OF'_1}} avec les données on a \frac{1}{-50} = \frac{1}{\overline{O_1A_1}} -  \frac{1}{30} Soit \frac{1}{\overline{O_1A_1}}= \frac{1}{-50} +  \frac{1}{30} = \frac{1}{75} Donc O_1A_1 = 75cm
\gamma_1 = \frac{75}{-50} = -1.5 Le grandissement est négatif et sa valeur absolue supérieure à 1 donc l'image est renversée et agrandie, de plus l'image est réelle car l'objet AB et placé avant une lentille convergente et le foyer focale f' derrière cette lentille.

2a) Je bloque ici car je ne vois pas où il faut utiliser la relation de Chasles. Mais je sais les 2 relations de conjugaison :
  
\frac{1}{\overline{O_1A_1}} - \frac{1}{\overline{O_1\infty } } = \frac{1}{\overline{O_1F'_1}}
\overline{O_1A_1} = \overline{O_1F'_1} = 30cm
et
\frac{1}{\overline{O_2F'_1}} - \frac{1}{\overline{O_2A_1 } } = \frac{1}{\overline{O_2F'_2}}
C'est ici que je ne sais pas comment poursuivre .
Je vous remercie d'avance pour votre aide.
Cordialement.

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 15-03-22 à 18:06

Bonjour
Ton énoncé est très détaillé et progressif...D'accord avec tes résultats de la première question.
Pour les relations de Chasles de la question 2 : tu connais les distances O1O2, O1F'1 et O2F2. Ta relation de Chasles doit faire intervenir O1, O2 comme points supplémentaires dans la relation.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 15-03-22 à 18:27

Je suis d'accord je me doutais qu'il fallait faire intervenir O1O2, mais je ne comprends pas comment faire apparaitre le F2F'1 la est mon problème pour la question 2b) je sais comment faire, on sait que O2F'1 = O2O1 + O1F'1
Donc \frac{1}{O_2A_1} = \frac{1}{O_2O_1 + O_1F'_1}-\frac{1}{O_2F'_2}
Soit \frac{1}{O_2A_1} = \frac{1}{-25 + 30 =5}-\frac{1}{50}
\frac{1}{O_2A_1} = \frac{1}{5}-\frac{1}{50} = \frac{9}{50}
O2A1 environ égale à 5.6 cm

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 15-03-22 à 19:11

\overline{F_{2}F'_{1}}=\overline{F_{2}O_{2}}+\overline{O_{2}O_{1}}+\overline{O_{1}F'_{1}}

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 15-03-22 à 19:18

Je n'avais pas pensé a utiliser deux fois la relation de Chasles deux fois, je vous remercie

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 16-03-22 à 12:30

Je ne comprend pas la question 2c) je ne comprends pas en quoi les points sont conjugués.
Pouvez-vous m'aider s'il vous plaît?

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 16-03-22 à 13:35

Pour étudier un doublet de lentilles, on procède de la façon suivante :
L1 donne de l'objet réel AB une image intermédiaire A1B1. On peut donc dire que A1 est le conjugué par L1 de A.
Ensuite, A1B1 peut être considérée comme objet pour la lentille L2 qui donne de A1B1 l'image définitive A'B'. On peut donc dire que A' est le conjugué de A1 par L2.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 16-03-22 à 13:38

D'accord mais je ne comprend pas ce qui en ressort dans les calculs, a moins qu'il faut que j'utilise la relation de conjugaison est-ce cela ?

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 16-03-22 à 15:57

Citation :
il faut que j'utilise la relation de conjugaison est-ce cela ?

Oui ; tu l'appliques à L1 sachant que A et A1 sont conjugués par cette lentille puis tu l'appliques à L2 sachant que A1 et A' sont conjugués par cette autre lentille.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 16-03-22 à 16:23

Donc si je ne me suis pas tromper  je trouve
La relation de conjugaison suivante

\frac{1}{O_2F'_1} - \frac{1}{O_2A_1} = \frac{1}{O_2A'}

Soit

\frac{1}{O_2O_1 + O_1F'_1} - \frac{1}{O_2A_1} = \frac{1}{O_2A'}
Donc
\frac{1}{-25} - \frac{9}{50} = \frac{1}{O_2A'}
Soit
\frac{-11}{50} = \frac{1}{O_2A'}
Donc
O_2A' = -4.55cm

Me suis-je tromper dans ma démarche ?

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 16-03-22 à 17:15

A1 conjugué de A par L1 :

\dfrac{1}{\overline{O_{1}F'_{1}}}=\dfrac{1}{\overline{O_{1}A_{1}}}-\dfrac{1}{\overline{O_{1}A}}

A' conjugué de A1 par L2 :

\dfrac{1}{\overline{O_{2}F'_{2}}}=\dfrac{1}{\overline{O_{2}A'}}-\dfrac{1}{\overline{O_{2}A_{1}}}

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 16-03-22 à 19:17

En corrigeant mes erreurs, je trouve que O_2A' = 25cm
et le grandissement par L2 lui vaut 1/2.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 16-03-22 à 20:02

Pour la question 2d) je trouve que \overline{O_1F} = \frac{-150}{11}\approx{-13,64}

Pour la question 2e) je trouve que \overline{O_2F'} = \frac{50}{11}\approx{4,55}

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 16-03-22 à 22:00

D'accord avec tes résultats. J'espère que tu saurais les justifier rigoureusement un jour d'examen ou de concours.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 17-03-22 à 13:58

Bonjour, j'ai un petit par rapport à la question 2c) (oui je retourne en arrière j'ai oublier une partie de la question...)
J'ai calculé le grandissement par rapport à L2, j'ai trouver 0.5 donc A'B' = 0.5* A1B1 mais je dois trouver le grandissement du doublet de lentille, sauf que je ne vois pas comment faire, je connais la formule générale du grandissement qui est \frac{OA'}{OA}
Mais je ne vois pas comment l'utiliser pour le doublet de lentille. Pouvez-vous m'aider s'il vous plaît ?

vanoise @ 16-03-2022 à 22:00

D'accord avec tes résultats. J'espère que tu saurais les justifier rigoureusement un jour d'examen ou de concours.

Bonjour Vanoise, voulez-vous voir la démarche que j'ai utilisé pour trouver les résultats ?

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 17-03-22 à 14:06

Grandissement du doublet :

\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{A'B'}}{\overline{A_{1}B_{1}}}\cdot\frac{\overline{A_{1}B_{1}}}{\overline{AB}}=\gamma_{2}.\gamma_{1}

Le grandissement du doublet est le produit des grandissements des deux lentilles.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 17-03-22 à 14:12

D'accord je vous remercie.
Donc \gamma_1 = -1.5 et \gamma_2 = 0.5
Donc mon grandissement finale est \gamma = -1.5 * 0.5 = -0.75
Soit l'image finale est rétrécie et renversée.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 17-03-22 à 15:08

Pour la question 3a) je remarque que F'1 et F2 sont confondus en un même point.
Pour la question 3c) je trouve via la figure 3 que j'ai utilisé, je trouve que l'image est virtuelle et renversée.

Mais je ne suis pas sûre que mon point B' soit juste...

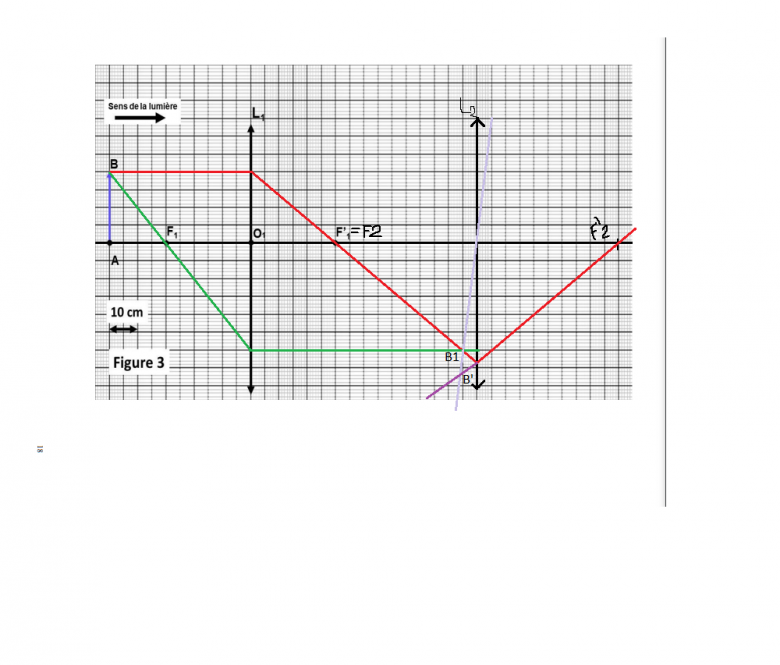
Doublet de lentilles\\ Optique géométrique

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 17-03-22 à 15:52

Pour 3a : le système est effectivement afocal : il donne d'un objet à l'infini une image à l'infini.
Concernant ta construction : tout va bien pour les deux rayons jusqu'à leur rencontre avec L2. Ensuite :
* le rayon "vert" arrivant sur L2 parallèle à l'axe optique ressort de L2 en passant par F'2 ;
* le rayon "rouge" passant par F2 ressort de L2 parallèlement à l'axe optique.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 17-03-22 à 16:13

D'accord je viens de corriger, j'aimerai savoir s'il vous plaît, si mes rayons violet utilisés pour trouver B' sont justes car je trouve que cela n'y est pas

Doublet de lentilles\\ Optique géométrique

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 17-03-22 à 17:15

Je ne comprends pas ce que viennent faire ici ces rayons "violets".
en sortant de L2 les rayons vert et rouge divergent. L'image de AB est donc virtuelle. B' est le prolongement des rayons vert et rouge (utiliser pour le tracé des pointillés vert et rouge). Tu obtiens A' comme le projeté orthogonal de B' sur l'axe optique.

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 17-03-22 à 17:42

B' est l'intersection des rayons "vert" et "rouge", mais il faut  prolonger les rayons vers la gauche afin de trouver B', d'où mes rayons "violets". Le "violet clair" passe par B1 et le centre optique O2 de la lentille L2
et l'autre et le prolongement virtuelle du rayon "vert".

Mon problème est que je ne sais pas s'il faut trouver que B1( que j'ai trouvé) ou alors il faut aussi trouver B' (que je suis pas sûr) car nous n'avons pas vu de système afocal  de 2 lentilles minces en cours. Je pense qu'il faut quand même trouver B' car A'B' est l'image final.

Posté par
vanoisere : Doublet de lentilles\ Optique géométrique 17-03-22 à 18:40

Effet de zoom au voisinage de L2 en me limitant aux deux rayons demandés par l'énoncé. On y voit clairement l'image définitive A'B'.

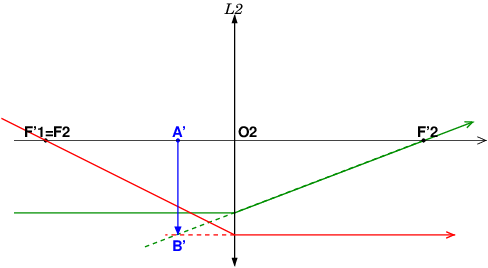
Doublet de lentilles\\ Optique géométrique

Posté par
tintin22re : Doublet de lentilles\ Optique géométrique 17-03-22 à 18:43

Oui c'est ce que j'essayais  d'expliquer, j'avais juste utiliser le rayon passant par le centre optique de O2.
Je vous remercie pour toute l'aide que vous m'avez apporté, bonne fin de journée à vous.

Posté par
Pauline08re : Doublet de lentilles\ Optique géométrique 18-03-22 à 12:34

Bonjour, je dois faire le même travail et j'ai réussi à le faire jusqu'à la question 2c)
En revanche je suis bloquée à la question 2D) celle où il faut calculer O1F, ainsi qu'à la question 2e) où il faut calculer O2F'
Je vois que tu as écrit les calculs mais je ne comprend pas comment tu as trouvé cela
Merci d'avance


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !