Bonjour
Il s'agit juste d'un indicateur coloré de fin de réaction.

Pour être plus précis, l'orthophénantroline forme avec les ions fer(II) un complexe de couleur rouge alors qu'elle forme avec les ions fer(III) un complexe bleu pale. Tu obtiens donc un changement de couleur à l'équivalence.

Je n'avais pas capté que le mélange fer(II) orthophénantroline était équimolaire. On ne peut pas alors considérer l'orthophénnantroline comme un simple indicateur coloré. As-tu enregistré la courbe potentiométrique E=f(V) ?
Je vais déjeuner et je reprends cela ensuite.

Je reprends mes explications en tenant compte du fait que la quantité initiale d'orthophénantroline est égale à la quantité initiale d'ion fer(II). Je suppose aussi le milieu suffisamment acide pour ne pas tenir compte des réactions de précipitation sous forme d'hydroxydes des ions fer(II) et fer(III).
La première réaction à se produire est celle faisant intervenir le plus grand écart de E° entre les couples. Il s'agit donc de la réaction entre les ions fer(II) et les ions Ce(IV) comme tu l'as écrit.
Une seconde réaction est possible entre les ions fer(II) complexés et les ions Ce(IV) : tu l'as écrite aussi.
Les E° permettent de déterminer les constantes d'équilibres de ces deux réactions. On constate deux choses :
* ces deux constantes sont très supérieures à 1 : les réactions peuvent être considérées comme quasi totales ;
* La seconde constante est très inférieure à la première : les deux réactions peuvent être considérées comme successives et indépendantes. Cela explique l'existence de deux sauts de potentiels donc de deux équivalences.
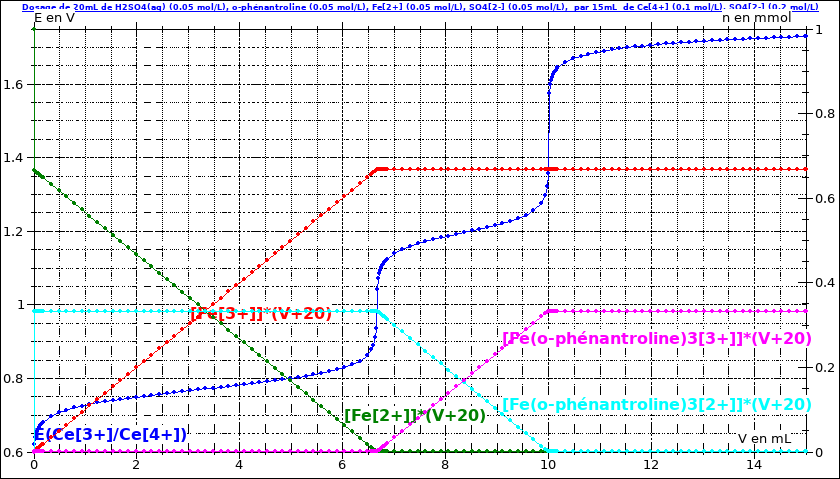
Tous cela est visualisé sur la simulation ci-dessous :
*en bleu la courbe E=f(V) montrant les deux équivalences
* les autres courbes représentent les variations des quantités (produit des concentrations par le volume totale (V+20)mL)...
Je te laisse examiner les courbes et vérifier qu'elles sont bien cohérentes avec ce qui a été écrit ci-dessus.
Tu peux remarquer que la première équivalence intervient pour un volume V ajouté égal au 2/3 du volume ajouté à la seconde équivalence. Cela signifie que, à partir d'un mélange équimolaire ions fer(II) - orthophénantroline,  seulement un tiers des ions fer(II) se complexent. Sachant que la réaction de complexation est totale, tu peux en déduire la valeur de n de la réaction :
Fe²⁺ +n (o-phen) [Fe(o-phen)_n]²⁺
(le résultat est écrit sur la courbe...)

Merci beaucoup pour votre réponse, cela m'a permis de comprendre les deux réactions en jeu, seulement, dans mon exercice je ne suis pas supposé avoir fait le dosage, je dois calculer théoriquement les deux équivalences, ainsi que les différences de potentiel aux deux demi équivalences et justifier que les deux sauts soient bien visibles.

Vous m'avez bien éclairé sur la partie expérimentale mais malheureusement je bute beaucoup sur la partie théoriques (bilans molaires etc..)

Merci de m'avoir aidé !

La seconde équivalence correspond au dosage de la totalité des ions fer(II) introduits : ceux non complexés et ceux complexés. Cela conduit à :
Co.Vo=C1.Ve2
Je t'ai justifié l'existence des deux équivalences : les deux constantes d'équilibre doivent être très supérieures à 1 et la seconde doit être très inférieure à la première. Je te laisse faire le calcul de ces deux constantes connaissant les trois valeurs des E°
Pour trouver le x (que j'ai malencontreusement noté "n" dans mon message précédent) il faut avoir fait le TP et constaté :
Commence déjà par bien comprendre tout cela puis essaie de trouver les potentiels de Nernst aux équivalences. La méthode générale est celle-ci : puisque la solution est à l'équilibre à chaque instant (cinétique hyper rapide pour ce genre de réaction), le potentiel mesuré de la solution est la valeur commune aux potentiels de Nernst des différents couples présents.

En fait, je trouve Co.Vo=C1.Veq1 à la première équivalence mais pour la 2ème équivalence je ne parviens pas à la faire avec la deuxième réaction.

Pour les constantes j'ai trouvé k1=10^(12,88) et k2=10^(6,44), ça me parait cohérent avec ce que vous avez dit (k1>>k2 donc réactions quasi totales et successives).

OK pour les constantes mais pas pour l'interprétation des deux équivalences. Comme déjà expliqué :
Lorsqu'on "fabrique" le mélange de sel de fer(II) et d'orthophénantroline. Une partie des ions fer(II) se complexe. La première équivalence correspond au dosage des ions fer(II) non complexés et la seconde équivalence correspond au dosage de tous les ions fer(II) initialement introduits : les ions non complexés et les ions complexés. Cela conduit donc à Co.Vo=C1.Veq2.
Puisque : : seulement un tiers des ions fer(II) initialement mis en solution ont réagit sur l'orthophénantroline. L'orthophénantroline et les ions fer(II) étant introduits dans la solution initiale en quantités égales, un rapide tableau d'avancement montre que le complexe a pour formule [Fe(o-phen)₃]²⁺ ; x=3 avec tes notations.