Inscription / Connexion Nouveau Sujet
Dm équation différentielle et de récurence
Bonjour,
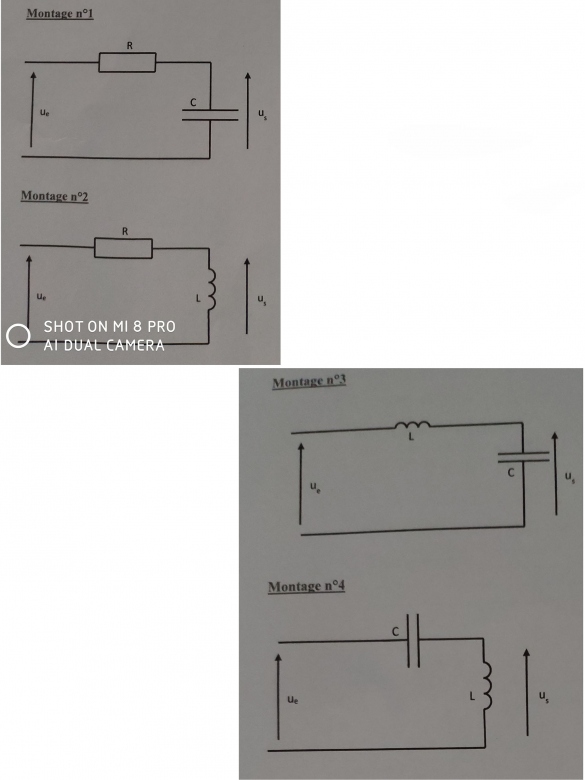
Pour ce DM il nous faut trouver l'équation différentielle et de récurence de chaques montages avec pour données :
R = 1.0 kOhm; L = 1.0 H; C = 1.0 uF et Te = 1.0 uS (Te étant la periode d'échantillonage)
on nous dit aussi que :
Ur = r . i; UL = L . di/dt et i = C . dUc/dt
et pour finir il nous faut l'équation de récurence sous la forme :
Yn = A0 . Xn + A1 . Xn-1 + A2 . Xn-2 + B1 . Yn-1 + B2 . Yn-2
Sachant que Ue(t) = Xn en numérique et Us(t) = Yn en numérique.
Ce que j'ai fait pour le moment :
Avec un peu d'aide j'ai pu déterminer que pour le montage n°1 l'équation différentielle était :
Ue(t) = RC . (dUs(t)/dt) + Us(t)
pour le second montage j'ai :
Tau . (dUe(t)/dt) = Tau . (dUs(t)/dt) + Us(t)
pour la 3ème j'ai :
(dUe(t)/dt) = L . Us(t) + (dUs(t)/dt)
(Je suis pas sur à 100% pour celle-ci)
et pour la 4ème j'ai :
Ue(t) = C . (dUc/dt) + Us(t)
(pareil je ne suis pas certain de celle-ci)
Voilà ou je bloque, même avec l'aide de mon cours, je ne trouve pas comment détèrminer cette équation de récurence, je ne vois rien de la sorte dans mon cours. J'ai bien des explications sur ce qu'est une équation de récurence mais pas d'explication sur comment la trouver avec ce que j'ai sur cet exercice.
Bonjour,
Le principe du passage équation différentielle / équation de récurrence consiste à approximer la dérivée avec
la période d'échantillonnage.
Bonjour,
J'ai répondu à la question sur la récurrence sans vérifier les équations.
Pour la 3 et la 4, il faut un auto-controle
1- le grand classique : vérifier l'homogénéité ; 3 et 4 ne sont pas homogènes
2- avec un peu plus d'habitude, dans 3 et 4 il y a deux origines distinctes de la dérivation, donc le système final doit être d'ordre deux.
Comment avez-vous obtenu les équations 3 et 4 ?
Bonjour,
j'ai simplement obtenu les équations en me référant aux précédentes et aux formules de UL et i données dans l'énoncé.
Après perso ce qui me dérange le plus c'est l'équation de récurrence. Je ne vois absolument pas comment la faire...
Bonjour,
Prenons 3 : i=C dUs/dt ; Ue=UL+Us=L di/dt+Us ; on remplace i par sa valeur et on obtient ?
Pour l'équation de récurrence, que ne comprenez-vous pas dans mon indication ?
Bah si on remplace i par sa valeur on obtiens C . dUs/dt non ?
Euh bah j'ai rien compris a vos indications en fait
Bonjour,
"Bah si on remplace i par sa valeur on obtiens C . dUs/dt non ?"
Oui c'est bien cela et en remplaçant dans Ue=L di/dt+Us cela donne quoi ?
"Euh bah j'ai rien compris a vos indications en fait"
Equation 1 : Ue(t) = RC . (dUs(t)/dt) + Us(t) que l'on prend à l'instant (n Te) donne
(1) Xn = RC (dUs/dt)(t=nTe) + Yn
On approxime la dérivée dUs/dt en disant que cela vaut approximativement , c'est là que cela coince ? (niveau autre ne permet de savoir si c'est évident ou pas pour vous).
Ensuite , même question.
soit et il reste à reporter dans (1)
Alors, pour commencer dans Ue=L di/dt+Us cela devrais donner quelque chose comme :
Ue=L (dC . Us/dt)/dt+Us ?
ensuite j'avais bien compris qu'il fallait remplacer Xn par nos équations de récurrence mais ce que je ne comprend pas c'est comment obtenir cette équation justement ?
par exemple, il faudrait que je fasse :
Yn = RC (dUs/dt)(t=nTe) + (Yn + RC (dUs/dt)(t=nTe) + Yn)^-1... ?
Ue=L (dC . Us/dt)/dt+Us ? Oui, mais terminez les calculs pour avoir qqch de lisible.
" comment obtenir cette équation justement ? "
C'est l'objet de mon message de 14:43 pas assez détaillé ?
"Yn = RC (dUs/dt)(t=nTe) + (Yn + RC (dUs/dt)(t=nTe) + Yn)^-1... ?"
La relation que je vous ai indiquée Xn = RC (dUs/dt)(t=nTe) + Yn (après remplacement de la dérivée) est de la forme désirée : équation de récurrence. A quoi correspond votre calcul ? Le Yn à gauche est un Xn et vous remplacez le Yn final par
Oui mais non dans l'énoncé c'est préciser qu'il faut qu'elle soit de la forme
Yn = A0 . Xn + A1 . Xn-1 + A2 . Xn-2 + B1 . Yn-1 + B2 . Yn-2
(désolé j'étais sur de l'avoir préciser dans mon texte de départ)
"Ue=L (dC . Us/dt)/dt+Us ? Oui, mais terminez les calculs pour avoir qqch de lisible."
comment ça ?
"il faut qu'elle soit de la forme Yn = A0 . Xn + A1 . Xn-1 + A2 . Xn-2 + B1 . Yn-1 + B2 . Yn-2"
Yn = Xn + 0.8 Xn-1 (au hasard) est bien de la forme attendue avec A2=B1=B2=0.
On peut laisser tomber la dérivée seconde : on peut obtenir l'équation de récurrence à partir des équations intermédiaires.
On va revenir sur la dérivée : pour vous que signifie dUs/dt ?
Dérivée de Us par rapport au temps, oui, mais quelle est la signification de la dérivée, ceci pour arriver à :
Alors la je sais pas, moi tout ce que je souhaite c'est réussir à faire quelque chose avec ces équations de récurences....
Bonsoir,
Dans quel cadre avez-vous cet exercice ?
La dérivée de y par rapport à t indique comment varie y quand t varie, la signification de dy/dt est contenue dans sa notation, c'est le rapport entre la variation de y et la variation de t pour de faibles variations (j'espère qu'il n'y a pas de mathématicien en ligne...).
La variation de y entre (n-1)Te et nTe est (Yn - Yn-1) et la variation de t est Te.
Ce qui donne
Il n'y a pas de contexte particulier il s'agit simplement d'un DM dans le cadre d'un BTS SNIR seconde année.
Oui sa je suis d'accord mais du coup pour l'équation de récurrence je fais comment ? concrètement comment je la sort ?
On reprend à partir de Xn = RC (dUs/dt)(t=nTe) + Yn et dUs/dt=(Yn - Yn-1)/Te ; soit
Xn=RC * (Yn - Yn-1)/Te + Yn
soit
Yn(RC/Te+1)=Xn+RC/Te Yn-1
soit
Yn=Xn /(RC/Te+1) +Yn-1 RC/Te/(RC/Te+1)
qui est bien de la forme voulue (calculs à vérifier !)
Remarque : encore des réflexes à acquérir : j'avais d'abord trouvé /(RC/Te-1) qui diverge si RC=Te et il n'y a pas de raison, donc vérification ...
D'accord je commence à y voir plus clair je vais essayer de me débrouiller pour les suivantes merci pour ton aide et tes conseils.
(remarque à mon tour : Heureusement je ne souhaite pas continuer dans la physique, en réalité c'est un cours obligatoire dans ma formation mais qui n'a rien à voir avec le but de la formation, de base on est tous censé vouloir finir soit programmeur informatique (mon cas, le développement d'applications et de sites web c'est mon truc) ou alors dans le réseau c'est à dire développer des réseaux d'entreprise etc...)


