Inscription / Connexion Nouveau Sujet
Dm électromagnétisme
Bonjour, Voici un dm qui ma été donné, je suis actuellement en 2e annee ingenieur
Je ne demande pas de laide sur tout
Jau surtout des difficultés sur lexercice 1 je nai aucune idee a part que le champ serait une ligne ou un point le long de l'axe phi
Jai surtout un gros pb pour résoudre lexercice 2
Sur la question des flux (4) et (5)
Je ne sais juste pas comment calculer le flux du champ E sur les bases, javais eu l'hypothèse de sortir E de l'intégrale (mais je ne sais pas si jai le droit) et d'intégrer dS ce qui donne S donc pi×r² et donc ainsi de multiplier par E que jai trouvé dans les questions précédentes(1)
Pour le dernier exercice j'ai des difficultés sur les 2 dernières questions je n'ai pas du tout vu la forme ellipsoïdale en cours et pour la question 4) jai pensé a prendre lexpression du flux (double intégrale de E.dS) et le sortir de l'intégrale et donc donc de multiplier lexpression de E trouvé en question 1) par S qui est pi×r² mais je ne pense pas que cela soit correcte
On considère un champ vectoriel W qui en coordonnées sphériques (r, teta,phi) n'a qu'une composante non-nulle Wphi indépendant de la coordonnée phi
1) quelle est la nature des lignes de champ? pourquoi ?
2) ce champ correspond-t-il à un champ électrostatique effectivement réalisable?
3) pour la question de la réponse donnée est négative indiquer sur quelle propriété elle est fondée. Si la réponse est positive donner un exemple de système créant un tel champ
Soit le potentiel electrostatique V=Vo(x²+y²-2z²)
1) déterminer les composantes du champ électrostatique qui en dérive
2) déterminer l'allure des courbes équipotentielles et l'allure des lignes de champ dans le plan ou (z=0)
3) calculer la divergence du champ en un point quelconque de l'espace. Que peut-on dire de son flux à travers une surface fermée?
4) Soit un cylindre d'axe Oz, de rayon R, limité par des plans z=0 et z=a
calculer le flux du champ à travers chacune des deux surface de base du cylindre on précisera l'orientation choisi pour la surface 5) calculer le flux du champ à travers surface latérale du cylindre
Un conducteur à l'équilibre sphérique, de centre O, de rayon R et de capacité C est chargé avec une charge Q>0. soit Sf une surface sphérisue de centre O et de rayon R. 1) donner la valeur de champ électrique à l'intérieur du conducteur
2) décrire le potentiel electrostatique au sein du conducteur et donner son expression en fonction de C et de Q
3) décrire la distribution de charges au sein du conducteur
4) donner la valeur du flux du champ électrostatique à travers Sf dans les cas r<R et r>R
5) si la forme du conducteur est ellipsoïdale comment la distribution de charge change-t-elle?
Merci par avance de toute l'attention que vous porterez à ce poste
Bonjour,
Le multi-compte est strictement interdit sur le forum 
:
Merci donc de régulariser ta situation en supprimant ton compte inestaillieu.
Une fois que ce sera fait, contacte malou ou moi.
Bonjour,
1) Un champ n'est ni une ligne ni un point c'est un vecteur. Ce qu'on cherche est la ligne de champ parallèle à ce vecteur.
2) Effectivement réalisable veut dire obéissant au règle gouvernant E : autrement dit les équations de Maxwell.
Remarque : il y a 36 1) 2) ... c'est difficile de vous répondre ...
J'avais eu l'hypothèse de sortir E de l'intégrale (mais je ne sais pas si jai le droit) et d'intégrer dS ce qui donne S donc pi×r²
pour lex 3, il s'agit donc de vecteurs horizontaux est-ce cela?
dans mon cours je n'ai malheureusement pas vu les 4 equations de maxwell enfin du moins la dernière et je ne sais pas comment appliquer les autres j'ai regardé sur internet et ils parlent de champ magnétique et électrique or ici il n'est question que d'un seul champ non?
(quand je précise Q1 ou Q2,... j'ai précisé au dessus à quel exercice j'étais 1, 2 ou 3)
et a propos de l'ex2, pour les bases dS est orienté dans le sens de l'axe Oz et dans la première question j'ai trouvé E = -2Vox ex -2Voy ey +4Voz ez
E n'est donc pas constant et je ne peux pas le sortir de l'intégrale mais du coup jai un produit scalaire entre le champ qui s'exprime en focntion x, y et z et le Ds en fonction de Z je ne multiplie donc que les coordonées selon z ensemble?
Bonjour,
Pour les lignes de champ, dessiner . Quelles sont les lignes qui sont constamment tangentes à ce vecteur ?
Une fois cette ligne trouvée, quelle propriété connaissez-vous sur les lignes de champ électriques, concernant par exemple le potentiel ?
pour lex 3, il s'agit donc de vecteurs horizontaux est-ce cela?
Dans l'exercice 3, il est question d'une sphère, je ne vois pas en quoi l'horizontale pourrait jouer un rôle.
Dans l'ensemble, il n'est en effet question que de champ électrique statique.
Pour le flux, commencez par effectuer le produit scalaire (je suppose que c'est que veut dire "je ne multiplie donc que les coordonnées selon z ensemble ?". Cela donne quoi pour les bases du cylindre ? Est-ce que le résultat est constant sur la surface ?
Pour la surface latérale idem, pour "voir" le produit scalaire, un dessin vu de dessus du cylindre peut aider à trouver
Je ne vois vraiment pas pour le flux quelle expression de E prendre, celle de la question 1 donc en fonction de x y et z ou alors seule la composante selon z est uniquement à prendre en compte? et puis pour ds
À quoi est égal ds?
Dxdy ?
Dans ce cas je trouve bête de prendr seulement le composante selon z, peut-être je devrais prendre celles ce x et y non?
En fait je ne sais vraiment multiplier quoi par quoi
Bonjour,
Dans l'exercice 1, le champ a comme direction , pas vraiment horizontale.
L'expression de E est celle en effet de la première question.
Pour ce qui est de dS on pourrait détailler, mais ici, il n'en est nul besoin : dS est la surface élémentaire, l'aire de la surface infiniment petite prise autour de M, et cela suffit. Par contre il faut absolument que vous donniez le résultat de pour pouvoir avancer et donc que vaut ce produit scalaire ?
En fait je ne sais vraiment multiplier quoi par quoi
Il faut multiplier
Je sais bien que c'est cest E.dS, je connais mes formules or vous me demandez ce qu'est le produit scalaire mais que je n'ai pas besoin de connaître dS or pour faire E.dS il faut bien que je connaisse dS mais je ne sais pas ce que c'est
Et à propos de lisa hein je ne vois pas comment vous savez quelle est sa direction, comment savez vous que cest Uteta la composante non nulle est selon phi non?
Pour le 2, écrivez puis
, effectuer le produit scalaire : cela donne quoi ?
il faut bien que je connaisse dS
Pas nécessairement : si, comme vous le dites "javais eu l'hypothèse de sortir E de l'intégrale",
Et à propos de lisa hein je ne vois pas comment vous savez quelle est sa direction, comment savez vous que cest Uteta la composante non nulle est selon phi non?
Je suppose que lisa veut dire exercice 1, où ai-je écrit que la composante non nulle était selon
Pour lexercice 1 la seule composante qui a une valeur cest selon phi (cest la seule composante non nulle) cest ce que l'énoncé dit
Mais comment pouvez vous sortir E
Il dépend de x y et z qui ne sont pas constants
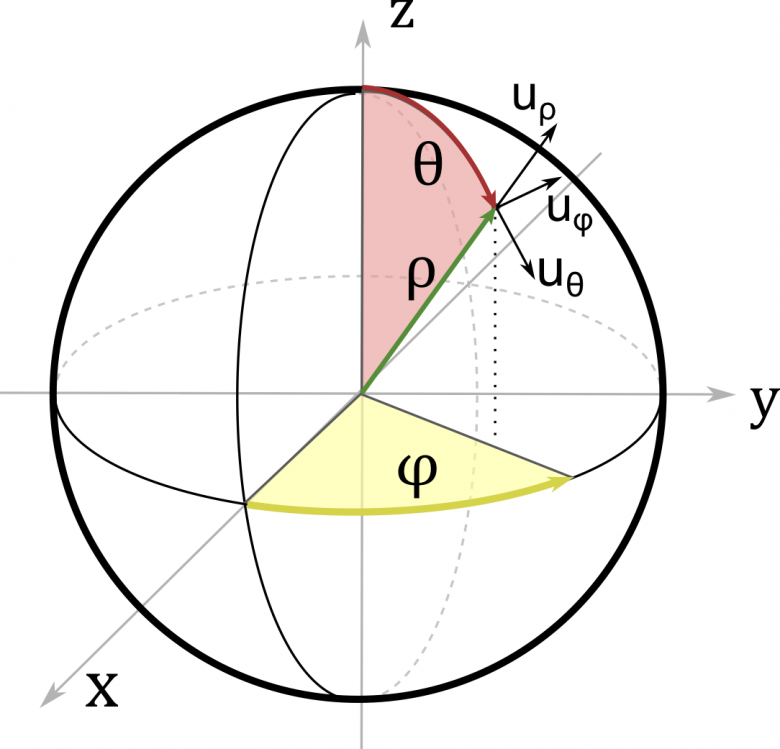
Pour l'exercice 1, on est d'accord, donc quelle est la courbe qui est constamment tangente à . Avoir sous les yeux les coordonnées polaires peut aider (d'après wikipedia) :
Mais comment pouvez vous sortir E, Il dépend de x y et z qui ne sont pas constants
La dépendance de E est sans intérêt, ce qui compte est la dépendance de
Je ne sais pas ce quil vaut vraiment pas sinon je vous aurez déjà répondu je suis complètement perdu vous me dite de sortir E et donc de faure E ×S
Et apres vous me demandez E.dS si je sors E de l'intégrale je nai pas besoin de connaitre ce produit scalaire
Etape 1 : (déjà fait) calcul de et
Etape 2 : produit scalaire (toujours pas effectué : quatrième demande)
Etape 3 : posez l'intégrale et voir si on peut sortir des termes de l'intégrale (oui !)
Etape 4 : sortir ce terme et faire apparaitre
Remarque : ne pas confondre et dS,
et E.
vous me dite de sortir E et donc de faire E × S
Soyons plus précis : votre idée de sortir des termes constants de l'intégrale est la bonne idée mais après avoir calculé le produit scalaire.
Je ne sais pas faire l'intégrale je vais essayer de me débrouiller
Integrale( 4z Uz × dS Uz)
= integrale(4z×dS)= 4z intégrale (dS) = 4z×S
=4a ×pi×r²
Et je ne donnais pas le scalaire aprce que je ne savais pas son expression car pour moi ce que jai écris au dessus est faux a ne peut pas sortir
C'est bien cela, il ne reste plus qu'à faire la même chose pour la surface latérale.
Sinon pour l'intégrale, voir l'aide ici : 
[lien] : bouton dans la barre de menus.
car pour moi ce que jai écris au dessus est faux a ne peut pas sortir
Ce que vous avez écrit est parfaitement juste, c'est quoi le "a" qui ne peut sortir ?
Integrale(E.dS)= integrale[(-2Vox Ux -2VoUy )× dS×(xcosteta + ysinteta)
xcosteta + ysinteta =dR
Et je suis bloqué parce que je ne suis pas sure de l'axe de dS mais a part R je ne vois pas ce sue ça peut-être
Peut-être qqch en fonction de x et y mais quoi donc
Bonsoir,
@Inest : gts2 t'a rappelé ceci :
extrait de 
la FAQ du forum :Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?
guide latex
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le 
mode d'emploi du forumTu as même un assistant Latex pour t'aider à le prendre en main :
Dans dS×(xcosteta + ysinteta) x veut dire Ux ?
xcosteta + ysinteta =dR n'est pas homogène différentielle d'un côté, terme fini de l'autre.
La direction de dS est bien .
Et quelle est la direction de ?
Cest Ur ? Je pense car dans le meme plan que le rayon
Merci beaucoup pour cet exercice mais je ne sais toujours pas comment résoudre lexercice 1
Le champ a seulement une composante selon Uphi mais je me demande cest seulement le long de l'axe où ça peut-être aussi en hauteur parallèle à l'axe?
La direction de est bien en effet
, donc le produit scalaire avec le vecteur surface sera simple. On peut même aller un peu plus loin, comment interpréter
en coordonnées cylindriques ?
Le champ a seulement une composante selon Uphi mais je me demande cest seulement le long de l'axe où ça peut-être aussi en hauteur parallèle à l'axe ?
Là je ne comprends pas la question :
"En hauteur parallèle à l'axe" là je n'arrive pas à interpréter.
Donc je réécris le texte : en tout point de l'espace
Vous reportez ce vecteur sur la figure de wikipedia (14:31) et vous cherchez une courbe constamment tangente (c'est une courbe simple).
@Inest : je viens de me rendre compte que tu n'as pas respecté une nouvelle règle, ça commence à bien faire : 1 sujet = 1 exercice 
=> avertissement.
La prochaine fois, je t'exclus pour une durée déterminée ...
@gts2 : quand ce genre de situation arrivent, je te remercie de refuser de répondre jusqu'à ce que l'aidant ce soit mis en règle comme annoncé en début d'année : Mise à jour de la FAQ et rappels
Tu peux soit me faire un signalement, soit rappeler les règles via ce résumé : [***A LIRE AVANT D'AGIR***] Règles du forum
C'est trop tard pour le coup ici de scinder le sujet
@gbm : OK compris.
J'en profite pour te remercier du travail de modération du site.
Merci pour ton retour et tes encouragements. Votre soutien dans la modération est d'autant plus important qu'on se trouve en plein dans le traditionnel pic annuel d'activité : on est sur tous les fronts !
J'ose croire que cet investissement contribue à maintenir un forum de qualité, au sein duquel nous aimons aider, échanger, progresser, faire progresser, ...
Bonne soirée
!Bonjour, Voici un dm qui ma été donné, je suis actuellement en 2e annee ingenieur
Jau surtout des difficultés sur lexercice 1 je nai aucune idee a part que le champ serait un vecteur sur l'axe phi car il ne peut-être dans l'espace vu quil na que une seule composante
On considère un champ vectoriel W qui en coordonnées sphériques (r, teta,phi) n'a qu'une composante non-nulle Wphi indépendant de la coordonnée phi
1) quelle est la nature des lignes de champ? pourquoi ?
2) ce champ correspond-t-il à un champ électrostatique effectivement réalisable?
3) pour la question de la réponse donnée est négative indiquer sur quelle propriété elle est fondée. Si la réponse est positive donner un exemple de système créant un tel champ
Merci par avance
*** message déplacé ***
Bonsoir
Et si tu expliquais ce que tu as réussi à faire et ce qui te bloque ? Plus facile de t'aider ensuite !
*** message déplacé ***
@Taillieu : ce n'est pas en supprimant ton précédent compte et en créant un nouveau dans la foulée que tu vas retrouver une virginité ...
Tu t'entêtes à ne pas vouloir respecter les règles : [***A LIRE AVANT D'AGIR***] Règles du forum
) :
Cette fois-ci c'est une exclusion ...
J'avais bien précisé ceci dans mon message du 27-10-20 à 20:26 :
C'est trop tard pour le coup ici de scinder le sujet
Bonjour,
Je suis très peu inspiré par un exercice qui m'a été donné, le voici :
On considère un champ vectoriel W qui en coordonnées sphériques (r, teta,phi) n'a qu'une composante non-nulle Wphi indépendant de la coordonnée phi
1) quelle est la nature des lignes de champ? pourquoi ?
2) ce champ correspond-t-il à un champ électrostatique effectivement réalisable?
3) pour la question de la réponse donnée est négative indiquer sur quelle propriété elle est fondée. Si la réponse est positive donner un exemple de système créant un tel champ
Pour la Q1 je me suis dis que le champ est une courbe simple dans le plan r,teta
Le champ s'écrit W=W(r,teta)Uphi
Pour la 2 je pense que ce champ est réalisable
Mais pour la 3 je n'ai aucune idée
Mais en faut j'ai du mal à me dire que le champ na que une composante selon phi mais je depend pas de celle ci et du coup je ne sais pas si cest une courbe comme je l'ai dis cela me parait bizarre
Merci par avance de l'aide que vous m'apporterez
*** message déplacé ***
Bonjour,
Vous avez régularisé votre situation ?
Pour 2) "je pense que" n'est pas une réponse ... d'autant plus que la réponse est fausse.
3) est juste la rédaction de 2), donc si vous ne pouvez répondre à 3) vous ne pouvez répondre à 2).
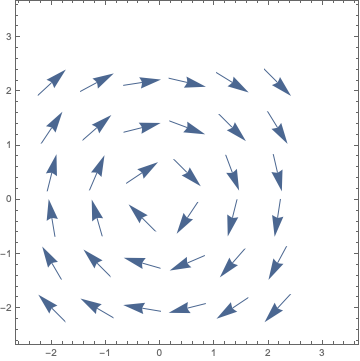
Pour 1) un champ n'est pas une courbe mais une fonction vectorielle définie en tout point. Traduit visuellement vu de dessus (dans la direction opposée à Oz donc), cela donne :
*** message déplacé ***
Je ne vois pas pq vous parlez de z il nest pas dans le système de coordonnées spherique
Et je ne vois pas comment le champ peut avoir cette forme il est dans un plan ainsi pour moi il a 2 coordonnees et non une seule
*** message déplacé ***
Mais donc les lignes de champ sont des vecteurs mais est ce qye cela est une nature?
*** message déplacé ***
En coordonnées sphériques, l'axe Oz est l'axe "vertical".
Le fait qu'il soit dans un plan (avec deux coordonnées x et y, c'est normal pour un plan non ?), c'est pour vous faciliter la représentation parce qu'en 3D c'est peu lisible.
Les lignes de champ ne sont pas des vecteurs, mais des lignes comme leur nom l'indique et qui sont en tout point tangent au champ. A la vue de l'image précédente, cette ligne me parait couler de source, non ?
*** message déplacé ***
Non je ne vois vraiment pas peut etre cest les lignes dans la direction de z? Ou laxe z?
De plus laxe z ne faut pas partie du « repère » spherique cest phi, teta et r
*** message déplacé ***
En cours et en td nous n'avons jamais fait de visualisation de champ ou meme essayer de comprendre leur forme et j'ai de plus de grosses difficultés alors pour moi ca ne coule pas de source desole
*** message déplacé ***
Annuler
connectez vous