Inscription / Connexion Nouveau Sujet
Dm de physique
Bonsoir,
Je voudrais avoir un peu d'aide dans ces exercices de physique.
Nous allons maintenant supposer que les deux masses sont en mouvement (c'est-a`-dire que m ≥ mmin). On note v = z ̇ la vitesse de la masse m. On suppose qu'`a l'instant initial la vitesse est nulle.
Nous cherchons `a calculer la vitesse des masses apr`es que celles-ci se soient déplacées d'une distante l.
1. Donner une justification physique pour expliquer pourquoi la vitesse de la masse m′ est ́egale a` la vitesse de la masse m c'est a` dire x ̇ = z ̇ = v. Nous supposerons cette relation v ́erifi ́ee par la suite.
J'ai justifié avec le constat de Galilée en disant que 2 corps de masses différentes chutent à la même vitesses.
2. Justifier pourquoi la norme de la tension du caˆble T = T ′ est constante.
J'ai aucune idée !
3. Ecrire le théoreme de l' ́energie cinétique appliqué `a la masse m et donner l'expression de
l' ́energie cinétique de la masse m en fonction de m, g, l et T.
J'ai répondu
Théorème de Energie cinétique est DeltaEc=SommeWF
Ec=mgl+T
4. Ecrire le théoreme de l' ́energie cinétique appliqué a la masse m′ et donner l'expression de
l' ́energie cinetique de la masse m′ en fonction de m′, g, l, T, kd et β.
J'ai répondu Ec=m'gl+T.kdcosB
5. A partir des deux ́equations calcul ́es en 3. et 4., donner l'expression de la vitesse v en fonction
deg,l,m,m′,kd etβ.
J'ai aucune idée
6. A partir des deux ́équations calculéden en 3. et 4. montrer que la tension du caˆble s' ́ecrit
T = g. mm'/m+m′ (1+sinβ+kdcosβ) (1)
J'ai aucune idée vu que je suis pas sûr de mes résultats
8. Sachant qu'un câble en acier à une résistance typique de 1700 N.mm−2 en déduquez le diamêtre minimum du câble.
J'ai mis la relation de la résistance.
Merci d'avance pour votre aide
Il n'y a pas grand chose de correct.
Je présume qu'il s'agit de ceci (mais c'eut été mieux que ce soit clairement indiqué).
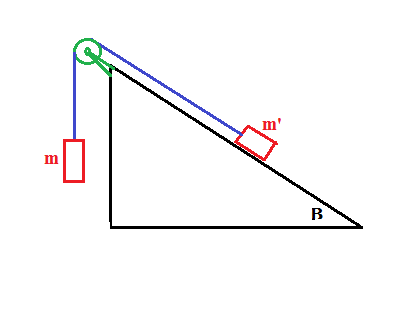
En négligeant le moment d'inertie de la poulie autour de son axe ...
Mais cela devrait aussi faire partie de l'énoncé.
1)
Câble supposé non extensible et donc ...
2)
Cherche
3)
mg.L - T*L = 1/2.m.(Vm)²
4)
Réaction normale du plan sur l'objet de masse m' : N = m'.g.cos(beta)
Force de frottement de l'objet de masse m' sur le plan incliné : f = kd.N = kd.m'.g.cos(beta)
avec kd le coefficient de frottement dynamique entre le plan incliné et l'objet de masse m'.
T*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L = 1/2.m'.(Vm')²
5)de T*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L = 1/2.m'.(Vm')² avec Vm' = Vm
--> Vm = ...
6)
(Vm)² = 2.(mg.L - T*L)/m
(Vm')² = 2.(T*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L)/m'
Et comme Vm = Vm', on a :
2.(mg.L - T*L)/m = 2.(T*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L)/m'
(mg - T)/m = (T - m'g.sin(beta) - kd.m'.g.cos(beta))/m'
m'.(mg - T) = m.(T - m'g.sin(beta) - kd.m'.g.cos(beta))
T(m+m') = mm'g + mm'g.sin(beta) - kd.mm'.g.cos(beta)
T = mm'g/(m+m') * (1 + sin(beta) + kd.cos(beta))
Recopier sans comprendre est inutile.
Sauf distraction. 
Merci pour votre aide.
Mais je comprends pas pourquoi dans la question 3 et 4 obtenir 2 fois le L
J'ai su répondre à la question 2.
Et je ne comprend pas d'où sort le Vm dans la question 6.
Merci d'avance.

3)
L'objet de masse m est soumis à 2 forces, son poids P et la traction de la corde T (vers le haut)
Le travail de ces 2 forces lorsque l'objet descend de la longueur L est W = P*L - T * L = mgL - T.L
Comme au départ (avant de descendre de la longueur L), la vitesse était nulle, on a (en appelant Vm la vitesse de l'objet après une descente de L) :
mgL - T.L = 1/2.m.(Vm)² (1)
4)
La somme des travaux des forces agissant sur l'objet de masse m' sur la distance L = Energie cinétique de l'objet en fin de distance L parcourue.
Cela donne : T'*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L = 1/2.m'.(Vm')²
Mais comme T' = T, on peut écrire :
T*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L = 1/2.m'.(Vm')² (2)
6)
On a déjà trouvé les 2 équations (1) et (2) :
mgL - T.L = 1/2.m.(Vm)²
T*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L = 1/2.m'.(Vm')²
qui donnent :
(Vm)² = 2.(mg.L - T*L)/m
(Vm')² = 2.(T*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L)/m'
Mais comme on sait que le mobile de masse m se déplace avec la même vitesse (en module) que le mobile de masse m', on a : Vm = Vm' et donc :
2.(mg.L - T*L)/m = 2.(T*L - m'g.sin(beta)*L - kd.m'.g.cos(beta)*L)/m'
...
Sauf distraction. 


