Inscription / Connexion Nouveau Sujet
Dipôles RC série et parallèle
Bonjour,
j'ai beaucoup de mal avec l'exercice suivant :
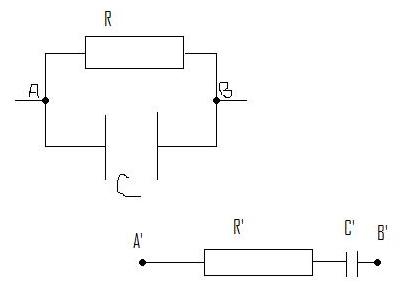
On considère les deux dipôles AB et A'B' alimentés en courant sinusoidal à la pulsation 
1.) Déterminer les expressions de C' et de R' pour que les impédances complexes des dipôles AB et A'B' soient identiques
2.) Pour quelle pulsation  a-t-on RC = R'C' ?
a-t-on RC = R'C' ?
Je ne vois pas quoi faire !! Raisonner avec les résonances ? :/ ou bien d'abord poser toutes les impédances des circuits ? 
Merci de votre aide
Bonsoir.
C'est assez classique comme démarche :
1 - exprimer l'impédance complexe de chaque circuit
2 - identifier les parties réelles et les parties imaginaires.
dipole AB : R en parallèle avec C :
impédance de R : Z = R , Y = 1/R
impédance de C : Zc = 1/jcw admittance : Yc = jcw
dipôle A'B' : pareil pour ce qui est de chacun des constituants :
pour AB, il faut d'abord que je travaille avec les admittances ?
Bonjour,
dipole AB : Y= 1/R + jC = (1 + Rjc
= (1 + Rjc )/(R), d'où :
)/(R), d'où :
Z = (R) / ( 1 + Rjc )
)
Dipôle A'B' : Z = R' + 1/(jc )
)
Mais ensuite je suis bloqué, je n'arrive pas à identifier les parties réelles et imaginaires.
Si on prend par exemple un nombre complexe z = a + bi
a est la partie réelle et b la partie imaginaire, or dans les deux expressions j'ai l'impression qu'on a, à part R, des parties imaginaires.

1)
1/Z(AB) = 1/R + 1/(1/(jwC)) = 1/R + jwC = (1 + jwRC)/R
Z(AB) = R/(1+jwRC)
Z(A'B') = R' + 1/(jwC')
Z(A'B') = (1 + jwR'C')/(jwC')
Z(AB) = Z(A'B')
R/(1+jwRC) = (1 + jwR'C')/(jwC')
jwRC' = (1 + jwR'C').(1 + jwRC)
jwRC' = 1 + jwRC + jwR'C' - w²RR'CC'
jwRC' = 1 - w²RR'CC' + jw(RC + R'C')
Il faut donc que le système suivant soit satisfait:
1 - w²RR'CC'= 0
RC' = RC + R'C'
C' = RC/(R-R')
1 - w²RR'CRC/(R-R') = 0
w²RR'CRC = R-R'
R'(1 + w²R²C²) = R
R' = R/(1+w²R²C²)
C' = RC/(R - R/(1+w²R²C²))
C' = C/(1 - 1/(1+w²R²C²))
C' = C.(1+w²R²C²)/(w²R²C²)
Groupement des résultats :
R' = R/(1+w²R²C²)
C' = C.(1+w²R²C²)/(w²R²C²)
-----
2)
RC = R'C'
RC = R/(1+w²R²C²) * C.(1+w²R²C²)/(w²R²C²)
RC = RC/(w²R²C²)
---> w²R²C² = 1
wRC = 1
w = 1/(RC)
-----
Recopier sans comprendre est inutile.
Sauf distraction (vérifie).