Inscription / Connexion Nouveau Sujet
dipole - cercle chargé
bonsoir
j'ai un cercle de charge répartie uniformément sur sa périphérie.
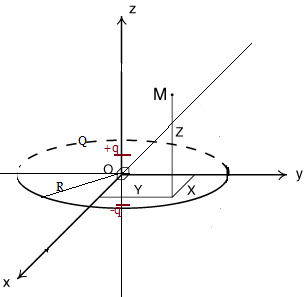
je cherche à déterminer les actions mécaniques subies par le dipôle en son centre
dans le cas où son moment dipolaire est colinéaire à et dans le cas où il est normale.
je ne vois pas comment commencer ...
merci de me donner des pistes si vous en avez
Bonsoir,
Une méthode possible : détermine l'expression du vecteur champ E en fonction de z.
Tu montreras ensuite que les actions sur le dipôle correspondent à un moment nul et à une résultante qui s'exprime simplement en fonction du moment dipolaire et de la dérivée de Ez par rapport à z (dérivée calculée en z = 0)
Bonsoir,
Une méthode possible : détermine l'expression du vecteur champ E en fonction de z.
tu veux dire avec des considérations symétriques ou explicitement ?
Les considérations sur les symétries de la source du champ (le cerceau chargé) vont te permettre de montrer qu'en tout point M de l'axe (Oz) de cote z, le vecteur champ créé par le cerceau chargé est colinéaire au vecteur unitaire Uz :
Il faudra ensuite, en intégrant l'expression générale du vecteur champ élémentaire, établir l'expression de Ez=f(z)
Ensuite, tu pourras montrer que l'action du cerceau chargé sur le dipôle se réduit à une force qui dépend du moment du dipôle et de :
d'accord avec les symétries j'ai bien les mêmes résultats que toi
je fais le reste merci pour les indices


