Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

diffusion de noyaux

Posté par
ferality 27-03-21 à 22:59

Bonjour à tous,

J'ai un problème de mécanique de niveau L2 physique, l'énoncé est le suivant :

Un noyau d'hélium (particule \alpha) de masse m_1 est envoyée vers un noyau d'or de masse m_2 situé en un point O. On a m_2 >> m_1.
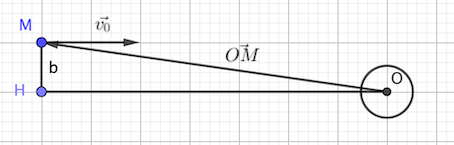
Bien avant l'interaction, en un point M_0, la particule \alpha a une vitesse \vec{v_0}. Le paramètre d'impact vaut b.

Les deux particules sont soumises à une force centrale répulsive de module F=K/r^2 qui dérive de l'énergie potentielle E=K/r (r est la distance entre les deux particules). L'étude est faite dans un référentiel galiléen (R) attaché à la masse m_2 qui est fixe.

a. Expliquer pourquoi la trajectoire de m_1 est plane dans ce référentiel

On voit dans cette ressource : que la raison est "parce qu'on a la conservation du moment cinétique", mais peut-être qu'il existe une explication plus complète et "compréhensible" ? Personnellement je ne comprend pas en quoi le fait que le moment cinétique se conserve implique que le mouvement est plan.

b. On appelle S le point de la trajectoire où la distance entre m_1 et m_2 est minimale. On pose r_m=OS Montrer qu'en ce point S les vecteurs \vec{OS} et \vec{V_S} sont orthogonaux. En déduire le module L_0(S) du moment cinétique (par rapport à O) de la particule lorsque celle-ci est située en S.

Je ne sais pas quoi faire du tout ici... prouver que le produit scalaire des deux vecteurs est nul \vec{OS}\cdot\vec{V_S}=0 ? Mais on ne dispose pas de l'expression des vecteurs dans le référentiel.

c. Calculer le module de L_0(M_0) du moment cinétique de la particule située en M_0. Comparer L_0(M_0) et L_0(S)

d. Ecrire l'énergie mécanique de la particule en S puis en M_0. Déduire des résultats précédents deux relations entre r_m et V_S. Calculer r_m en fonction des données du problème.


Merci d'avance pour votre aide

Posté par
gts2re : diffusion de noyaux 28-03-21 à 07:44

Bonjour,

a- que savez-vous de la relation "géométrique" entre  moment cinétique et la vitesse ?
Ensuite qu'est ce implique sur la vitesse le fait que moment cinétique soit constant.

b- Raisonnez éventuellement en coordonnées polaires pour la vitesse et traduisez  distance minimale.

c- Il s'agit d'une part de calculer les deux moments en utilisant les données et b et d'autre part d'utiliser a.

Posté par
feralityre : diffusion de noyaux 28-03-21 à 13:26

gts2 @ 28-03-2021 à 07:44

Bonjour,

a- que savez-vous de la relation "géométrique" entre  moment cinétique et la vitesse ?
Ensuite qu'est ce implique sur la vitesse le fait que moment cinétique soit constant.

Bonjour,
Je sais que le vecteur vitesse est toujours perpendiculaire au moment cinétique, car le moment cinétique est le produit vectoriel de la position par la vitesse (donc orthogonal à ces deux vecteurs). Donc la vitesse appartient toujours au plan dont le moment cinétique est un vecteur normal, donc le mouvement est plan.

gts2 @ 28-03-2021 à 07:44


b- Raisonnez éventuellement en coordonnées polaires pour la vitesse et traduisez  distance minimale.

Je dirais que le point "S" est le point auquel l'énergie potentielle centrale est maximale (car c'est le point le plus proche de O), donc r_{m}=K/E_{min}... mais on ne connaît pas E_{min} donc je ne sais pas si c'est utile de faire ça

Pour le vecteur vitesse, je dois trouver ses coordonnées en polaires à partir de O donc je dois calculer l'angle \phi_0 = arctan\dfrac{mbv_{\infty}^2}{K}, et ses coordonnées polaires seraient (phi_0, r_m)... après cela ne me donne pas ses coordonnées dans le repère polaire "local" où je devrais avoir juste \vec{V_S}=(expression)\vec{u_r}

Posté par
gts2re : diffusion de noyaux 28-03-21 à 14:54

a- OK
b- quelle est l'expression de v en polaires, et que peut-on en dire au minimum de r ?

Posté par
feralityre : diffusion de noyaux 28-03-21 à 16:04

gts2 @ 28-03-2021 à 14:54


b- quelle est l'expression de v en polaires, et que peut-on en dire au minimum de r ?


je dirais que \vec{V_S}=-V_S\vec{u_\theta} quand r est à son minimum. Quant à l'expression générale de V en polaires (sans être au minimum de r)... j'ai annoté le schéma pour montrer ce que je pense devoir faire, il faudrait avoir les angles (soit l'angle alpha soit l'angle beta) ?

diffusion de noyaux

Posté par
gts2re : diffusion de noyaux 28-03-21 à 16:10

\vec{V_S}=-V_S\vec{u_\theta}

C'est bien de là dont il faut partir.
Et donc le moment cinétique est immédiat.

Pour ce qui est de l'expression de la vitesse, vous ne connaissez pas \vec{v}=\dot r \vec{u_r}+ r\dot \theta \vec{u_\theta} ? Ceci étant, c'était juste pour vous amener à l'expression que vous avez trouvé puisque \dot r=0.

Posté par
feralityre : diffusion de noyaux 28-03-21 à 17:30

gts2 @ 28-03-2021 à 16:10

\vec{V_S}=-V_S\vec{u_\theta}

C'est bien de là dont il faut partir.
Et donc le moment cinétique est immédiat.


Alors ce que je trouve en b) c'est : \vec{OS}=r_m\vec{u_r} et \vec{V_S}=-V_S\vec{u_\theta}.

Ils sont orthogonaux, car \vec{OS}\cdot\vec{V_S}=r_m.0 + (-V_S).0=0

Pour le moment cinétique du point en S par rapport à O on a : L_O(S) = \vec{OS}\wedge m_1\vec{V_S} = m_1.||OS||.||V_S||.\sin(90°) = -m_1.r_m.V_S

C'est correct ?

gts2 @ 28-03-2021 à 16:10


Pour ce qui est de l'expression de la vitesse, vous ne connaissez pas \vec{v}=\dot r \vec{u_r}+ r\dot \theta \vec{u_\theta} ? Ceci étant, c'était juste pour vous amener à l'expression que vous avez trouvé puisque \dot r=0.


Oui je connais cette expression, mais je ne vois pas comment j'aurais pu l'utiliser pour trouver le résultat \vec{V_S}=-V_S\vec{u_\theta} ... je vois qu'on peut dire que quand r=r_m  alors \dot r devient nul, mais je ne vois pas ce que deviens \dot\theta à ce moment là... en fait j'arrive à \vec{V_S}=r_m\dot\theta\vec{{u_\theta}} et je ne sais pas comment avancer à partir de là pour arriver à l'expression de \vec{V_S} voulue.

Posté par
feralityre : diffusion de noyaux 28-03-21 à 17:35

Le moment cinétique est un vecteur donc ça serait en fait L_O(S) = -m_1.r_m.V_S.\vec{u_r}\wedge\vec{u_\theta} = -m_1.r_m.V_S.\vec{u_z}

Posté par
gts2re : diffusion de noyaux 28-03-21 à 17:41

La seule chose dont vous avez besoin est que la vitesse est perpendiculaire au rayon vecteur ce qui permet d'avoir un calcul du moment cinétique simple.

Votre moment cinétique est en gros exact, en gros car
- sin(90°)=+1
- il y a un mélange de vecteur et de scalaire
- l'angle (OS,V) vaut -90°

Sinon, on ne vous demande rien de plus que  L_O(S) =-m_1 \cdot r_m \cdot V_S
Donc vous pouvez passer à c)

Posté par
feralityre : diffusion de noyaux 28-03-21 à 18:11

D'accord, mais étant donné que c'est -90° et non 90°, sin(-90°)=-1 donc le signe du module du moment cinétique va s'inverser, je me trompe ?

Donc pour la c), il faut que je calcule L_O(M_0) = \vec{OM_0}\wedge\vec{v_0} On peut faire :

\vec{L_O(M_0)}=\vec{OM_0}\wedge\vec{v_0} = r\vec{u_r}\wedge(\dot{r}\vec{u_r}+r\dot{\theta}\vec{u_\theta}) = r\vec{u_r}\wedge\dot{r}\vec{u_r} + r\vec{u_r}\wedge r\dot{\theta}\vec{u_\theta} = r^2\dot\theta \vec{u_z}

Le résultat paraît un peu trop général par contre...

Posté par
gts2re : diffusion de noyaux 28-03-21 à 18:37

Il faut exprimer le moment en fonction des données :  vitesse \vec{v_0} et  paramètre d'impact b.

Pour le calcul du moment cinétique, il y avait deux erreurs de signe qui se compensaient.

Posté par
feralityre : diffusion de noyaux 28-03-21 à 18:57

D'accord donc je pose : \vec{v_0} = -v_0\cos\theta \vec{u_r} - v_0\sin\theta\vec{u_\theta}

\vec{L_O(M_0)}  = r\vec{u_r}\wedge(-v_0)\cos\theta\vec{u_r} - r\vec{u_r}\wedge v_0\sin\theta\vec{u_\theta} = - rv_0\sin\theta\vec{u_z} mais je n'arrive pas à faire intervenir le paramètre d'impact "b" désolé
J'ai l'impression que je dois forcément utiliser cette formule du cours pour l'angle (\vec{OM_0}, \vec{v_0}) :
\phi_0 = arctan\dfrac{mbv_{\infty}^2}{K} avec v_{\infty}=\vec{v_0} ...

Posté par
gts2re : diffusion de noyaux 28-03-21 à 19:03

Il faut faire simple :

- méthode 1 : technique du bras de levier
- méthode 2 : écrire \vec{OM}\wedge \vec{v_0} et décomposer le vecteur OM pour faire apparaitre le paramètre d'impact.  

Posté par
gts2re : diffusion de noyaux 28-03-21 à 19:19

Pour illustrer \vec{OM}=\vec{OH}+\vec{HM}
Cela revient à retrouver le bras de levier

diffusion de noyaux

Posté par
feralityre : diffusion de noyaux 28-03-21 à 19:40

D'accord, alors je connais la méthode du bras de levier pour les moments, mais pour le moment cinétique je ne connais pas de méthode à base de bras de levier... je serais curieux de savoir ce que c'est je ne trouve pas sur Google.

Après avec la méthode de somme de vecteurs, il suffirait de poser r^2=b^2+OH^2 donc on aurait : \vec{L_O(M_0)}  = - \sqrt{b^2+OH^2}.v_0.\sin\theta\vec{u_z}  

Posté par
gts2re : diffusion de noyaux 28-03-21 à 20:00

Un moment de force c'est \vec{OM}\wedge \vec{F}, un moment cinétique c'est \vec{OM}\wedge m \vec{v}, mathématiquement c'est la même chose, donc les méthodes utilisables sont les mêmes.

Méthode par décomposition  \vec{OM}\wedge \vec{v_0} =\vec{OH}\wedge \vec{v_0}+\vec{HM}\wedge \vec{v_0} or OH est parallèle à la vitesse, donc le terme correspondant est nul, soit  \vec{OM}\wedge \vec{v_0} = \vec{HM}\wedge \vec{v_0} et HM est perpendiculaire à la vitesse, donc le calcul est simple ...

Méthode en suivant votre piste (j'oublie les vecteurs pour alléger) : L=OM v sin( ), sur le dessin on voit que OM sin( )=-b,  

Posté par
feralityre : diffusion de noyaux 28-03-21 à 20:16

D'accord donc on a L_O(M_0) = -m_1.b.v_0 (car l'angle entre \vec{HM} et \vec{v_0} est -90°) ?

Posté par
feralityre : diffusion de noyaux 28-03-21 à 20:27

Et d'après a) on aurait L_O(M_0)=L_O(S)

Posté par
gts2re : diffusion de noyaux 28-03-21 à 20:37

C'est bien cela, et vous avez donc une première équation à deux inconnues rmin et vS
Il faut donc une deuxième équation, question d)

Posté par
feralityre : diffusion de noyaux 28-03-21 à 21:21

Alors on aurait pour les énergies mécaniques : E_m = E_c + E_p

E_m(M_0) = (1/2)m_1v_0^2 + K/r
E_m(S) = (1/2)m_1V_S^2 + K/r_m

La seule chose un peu dérangeante ici c'est le "r" dans "K/r" de l'énergie mécanique de M_0... j'ai pensé à le remplacer par \sqrt{b^2 + OH^2} mais pas sûr que ça soit judicieux

Posté par
gts2re : diffusion de noyaux 28-03-21 à 21:50

Le texte dit "bien avant l'interaction, ... " donc K/r=0.

Posté par
feralityre : diffusion de noyaux 28-03-21 à 22:18

D'accord désolé j'avais oublié ce détail important...

Par la conservation de l'énergie mécanique on a (1/2)m_1v_0^2 = (1/2)m_1V_S^2 + K/r_m, c'est notre deuxième relation entre r_m et V_S, et on résout le système suivant :

b.v_0.m_1 = r_m.V_S.m_1
(1/2)m_1v_0^2 = (1/2)m_1V_S^2 + K/r_m

Posté par
feralityre : diffusion de noyaux 28-03-21 à 22:42

je tombe sur : r_m = \dfrac{2K + b.v_0.m_1.V_S}{m_1.v_0^2}

Posté par
gts2re : diffusion de noyaux 29-03-21 à 05:28

Régle de base : exprimer le résultat en fonction des données, donc sans vS.

Posté par
feralityre : diffusion de noyaux 29-03-21 à 23:47

D'accord,

donc après avoir fait un binôme de second degré je trouve r_m = \dfrac{K + \sqrt{K^2+m_1^2b^2v_0^4}}{m_1v_0^2}.

Merci infiniment (encore ^^) pour votre aide gts2


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !