Inscription / Connexion Nouveau Sujet
Diffraction par ouverture circulaire
Bonjour,
Par curiosité je me suis intéressé à la diffraction, à peine touché par mon programme de physique qui s'arrêtait à donner la largeur de la tâche d'Airy sans démonstration.
Je suis bloqué au niveau du calcul, si quelqu'un peut me donner un coup de main ça serait cool et je vous en remercie d'avance.
Tout d'abord c'est la diffraction de Fraunhofer qui m'intéresse.
La formule de Fraunhofer donne pour l'amplitude résultante en M
où
est l'amplitude de l'onde sphérique émise en S
est le facteur de Kirchhoff (de ce que j'ai compris)
le chemin optique de S à M
et c'est le calcul de l'intégrale qui me gêne.
en effet le produit scalaire dans l'exponentielle donne :
et du coup l'intégrale à calculer est la suivante :
que je ne sais pas calculer. Google étant un ami j'ai regardé comment on faisait et beaucoup parlent des fonctions de Bessel. Notamment celles-ci :
la première
et la relation avec la deuxième
Le problème est que j'ai une intégrale double et j'ai, a priori deux fois le terme à l'intérieur de l'intégrale de Bessel mais je peux pas couper comme je veux cette intégrale .. Fin bref surtout un problème de Maths... du coup...
Conscient que ce sont les vacances, je serai toutefois reconnaissant envers celles et ceux qui répondront relativement rapidement.
Bonne journée
Bonjour Vanoise.
Plusieurs trucs.
Je pensais qu'en diffraction on n'était JAMAIS dans les conditions de Gauss???
Puis des lignes du calcul que je pige pas.
Tout d'abord je ne vois pas pourquoi est ce que l'on considère 2 rayons? un seul devrait suffire pour décrire le phénomène. Du moins pour la fente rectangulaire je l'ai fait facilement avec la formule de Fraunhofer (que je ne vois pas explicitement là) avec un seul rayon..
Puis pourquoi il affirme que le terme en sinus est nul? ça voudrait dire que
et je ne vois pas pourquoi..
Enfin je ne vois pas comment il reconnait sa fonction de Bessel. En effet si je regarde la formulation sur Wikipedia j'ai un cosinus d'une somme avec un sinus dans celle-ci.
Où est ce que je me suis planté?
Merci
Je pensais qu'en diffraction on n'était JAMAIS dans les conditions de Gauss???
Dans les conditions de Fraunhofer, le faisceau de lumière incidente est un faisceau de lumière parallèle créé soit par un laser soit par une source quasi ponctuelle placée au foyer d'une lentille convergente fonctionnant dans les conditions de Gauss.
De plus, le phénomène de diffraction est étudié à l'infini c'est à dire en pratique dans le plan focal d'une lentille convergente fonctionnant aussi dans les conditions de Gauss.
Parfois, l'objet diffractant est un diaphragme circulaire placé devant l'oculaire d'une lunette astronomique de façon que cet objectif fonctionne dans les conditions de Gauss... Je ne comprends pas d'où vient ce "JAMAIS" ; attention : je ne dis pas pour autant "toujours" : imagine un objet diffractant placé sur le plateau d'un goniomètre. En tournant la lunette d'observation réglée pour voir à l'infini, d'un angle
, on peut étudier la lumière diffractée dans cette direction et l'angle peut être grand : le fait de tourner la lunette la fait fonctionner dans les conditions de Gauss .
Tout d'abord je ne vois pas pourquoi est ce que l'on considère 2 rayons? un seul devrait suffire
Une phase est toujours définie à une constante près, un peu comme un potentiel ou une énergie potentielle ; seule la différence de phase a un sens physique. La phase qui intervient dans ta formule est en réalité la différence de phase entre l'onde reçue en M, diffractée par l'élément de surface d
centrée en P et l'onde reçue en M, diffractée par l'élément de surface d centrée en O.
Puis pourquoi il affirme que le terme en sinus est nul?
Un raisonnement sur la parité devrait suffire. Il n'est même pas nécessaire de supposer l'angle
petit mais comme expliqué plus haut, de nombreuses expériences correspondent à cette situation. Ne pas oublier (ce n'est pas dit sur le site) que l'axe (Oz) est axe de symétrie pour la figure de diffraction, d'où la simplification consistant à étudier la diffraction dans un plan...
Enfin je ne vois pas comment il reconnait sa fonction de Bessel
Un classique utilisé en physique :
J'avoue utiliser ce résultat sans le démontrer... Si tu veux des indications plus pertinentes, postes sur le forum de maths.
le "JAMAIS" c'est à cause de mon prof de physique de cette année. Je me faisait incendier quand je parlais de petits angles avec les réseaux ... et puisqu'il y a de la diffraction dans les réseaux j'ai fait l'amalgame dans trop réfléchir à la question. ^_^
ok pour la phase 
la parité en effet. Je suis à moitié aveugle, je ne vous avait pas prévenu ? :p
ok pour Bessel!
Je me faisait incendier quand je parlais de petits angles avec les réseaux
Il s'agit typiquement d'une situation où on peut étudier la diffraction avec
grand grâce à la rotation de la lunette d'un goniomètre !Oui en effet.
par contre encore une question sur le calcul. Dans le document est dit
L'amplitude Ax émise par un élément de surface du trou est
mais si c'est un élément de surface ça devrait être dxdy non?
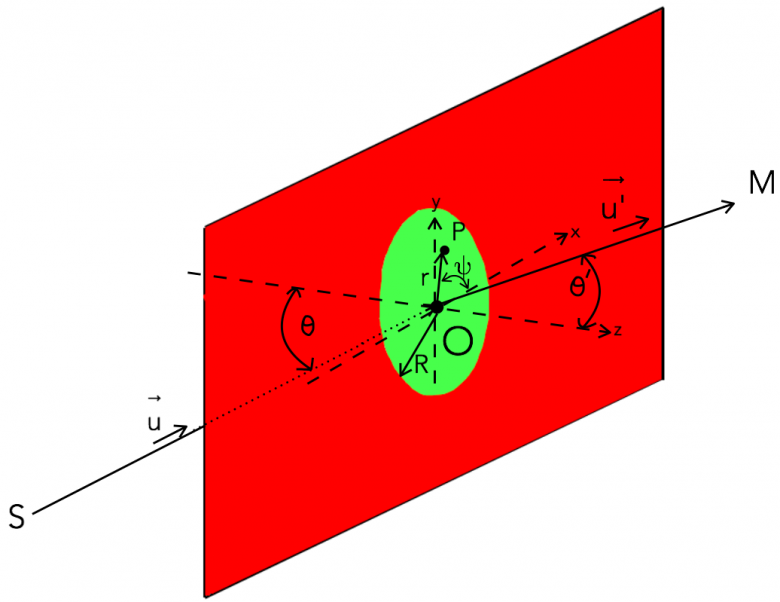
Compte tenu de l'axe de symétrie (O,z), on peut se limiter à l'étude de la diffraction dans le plan (Oxz) c'est à dire dans le plan de la figure de gauche. Le déphasage par rapport à une onde diffractée par un élément de surface contenant le centre O ne dépend que de x :
Tous les éléments de surface de la bande élémentaire comprise entre les abscisses x et (x+dx) créant des ondes en phase, l'auteur du site à « shunté » l'intégrale de surface en remarquant directement que cette bande a pour largeur . L'expression fournie est bien homogène et correcte. Il faut bien avouer que la rotation de 90° de la figure de droite (l'axe Ox vertical sur la figure de gauche est devenu horizontal sur la figure de droite) ne favorise pas la compréhension...
Annuler
connectez vous