Inscription / Connexion Nouveau Sujet
Difficulté Exercice Régime Sinusoïdale Permanent
Si une âme charitable a du temps pour m'aider ou m'expliquer car je suis bloquée... 
Même si vous savez répondre qu'à 1 ou 2 questions, je suis preneuse!
Voici l'exercice :
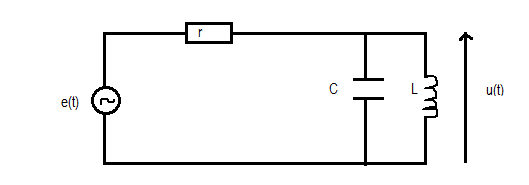
Un poste radio possède un filtre sélectif permettant de choisir et d'écouter une radio. Nous allons en étudier le principe avec le circuit suivant :
(Voir en bas)
Le signal reçu par l'antenne après amplification est modélisé par le générateur de Thévenin équivalent suivant: une source idéale de tension telle que e(t)=Ecos( t) et une résistance r en série.
t) et une résistance r en série.
1. En utilisant les modèles équivalents des dipôles à très basse et très haute fréquences, montrez que ce circuit correspond bien à un filtre passe-bande, c'est à dire que u(t) n'a pas de valeur non négligeable que sur une certaine plage de pulsations.
2. On posera notamment  0²=1/LC, Q=(L
0²=1/LC, Q=(L 0)/r et x=
0)/r et x= /
/ 0. Déterminer u(t) en régime sinusoïdal permanent en fonction de x, Q, E. Expliquez en quelques lignes pourquoi il faut préciser le régime dans lequel on se place.
0. Déterminer u(t) en régime sinusoïdal permanent en fonction de x, Q, E. Expliquez en quelques lignes pourquoi il faut préciser le régime dans lequel on se place.
3. Pour quelle pulsation que l'on notera  r, l'amplitude de u(t) est-elle maximale? Que vaut justement cette dernière à cette pulsation, ainsi que le déphasage par rapport à e(t)?
r, l'amplitude de u(t) est-elle maximale? Que vaut justement cette dernière à cette pulsation, ainsi que le déphasage par rapport à e(t)?
4. Définissez la bande-passante et déterminez-la. Quelle est sa "largeur" (c'est à dire la différence entre les deux pulsations limites de la bande passante)?
5. Une radio modulée en FM n'est pas une source de tension si simple que celle qui a servi à l'étude de ce circuit: elle est définie par une fréquence centrale fc (par exemple 87.8MHz pour France Inter sur Paris) et par tout une bande de fréquence autour de cette fréquence centrale notée  fc et qui vaut environ 0.1MHz. Si on considère que le circuit ne capte que les fréquences comprises dans la bande-passante, quel doit être Q pour que l'on capte bien France Inter? D'après vous, que se passe t-il si Q est trop grand? Trop petit? Sachant que L=10-4H et que la pulsation propre
fc et qui vaut environ 0.1MHz. Si on considère que le circuit ne capte que les fréquences comprises dans la bande-passante, quel doit être Q pour que l'on capte bien France Inter? D'après vous, que se passe t-il si Q est trop grand? Trop petit? Sachant que L=10-4H et que la pulsation propre  0 doit être de l'ordre de grandeur d'une pulsation centrale de radio, donnez l'ordre de grandeur de la résistance r.
0 doit être de l'ordre de grandeur d'une pulsation centrale de radio, donnez l'ordre de grandeur de la résistance r.
Merci d'avance 
Bonjour,
En BF, C est un circuit ouvert. Lw tend vers 0
En HF, L est un circuit ouvert. 1/Cw tend vers 0
Bonjour,
Les excellentes remarques de sanantonio devraient vous permettre de répondre au 1.
Pour la 2 exprimez u en fonction de e (en complexes) en utilisant une relation type "diviseur de tension".
A vous lire. JED.
Merci beaucoup pour vos réponses. 
Quand l'amplitude u(t) est maximale, ça signifie quoi? Enfin qu'est ce qu'on doit faire sur notre formule u(t)?
Bonjour,
A partir de l'expression de u en fonction de e en complexes passez aux modules.
Donc vous aurez U en fonction de E,Q et x.
Sauf erreur, pour x = 1 U sera maximale et égale à E.
u(t) et e(t) seront en phase.
A vérifier et à vous lire. JED.
Pour la question 1, je fais le modèle équivalent de tous les dipôles et je fais tendre Lw vers 0 puis en dans un second temps 1/Cw vers 0? Je ne suis pas sûre d'avoir bien compris :/
Je pensais qu'on avait fini avec la 1.
1: 
 0. L
0. L
 0 et 1/C
0 et 1/C

 . L//C
. L//C  0
0
2:

 . L
. L

 et 1/C
et 1/C
 0. L//C
0. L//C  0 aussi.
0 aussi.
L'impédance L//C ne tend donc pas vers 0 qu'à des fréquences intermédiaires.
Oui l'impédance j'ai trouvé ça aussi. Mais pour la suite je rajoute l'impédance de la résistance r aussi non? Pour trouver u(t)?
J'ai développé l'expression : [z/(z+r)] avec Z=jlw/1-LCw² et r dans l'expression U=(Z/Z+r)e puis, j'ai posé U=U0cos(wt+ ) = U0ejwt et d'après l'énoncé e(t)=Ecos(wt) = Eejwt. J'ai tout remplacé, à la fin ça me fait une expression de U0 assez énorme. Est-ce correct?
) = U0ejwt et d'après l'énoncé e(t)=Ecos(wt) = Eejwt. J'ai tout remplacé, à la fin ça me fait une expression de U0 assez énorme. Est-ce correct?
Après je fais le module de U0 et son argument puis je les intègre dans l'expression : U(t)=U0cos(wt+ ) pour avoir U(t)
) pour avoir U(t)
Je fais fausse route?
Bonsoir,
Gardez u = f(e)
Dans f vous aurez r ,L,C et w.
Introduisez LC, Q et x.
Vous obtiendrez u =g(e) en complexes. g contiendra x et Q.
Voilà pour la question 2.
JED.
Z/(Z+R)=(jLw/(1-LCw²))/((jLw/(1-LCw²))+R)
=jLw/(jLw+R(1-LCw²))
=jLw/(jLw+R(1-w²/w0²))
=jLw/(jLw+R(1-x²))
=(jLw/R)/((jLw/R)+(1-x²))
=(jQw/w0)/((jQw/w0)+(1-x²))
=jQx/(jQx+1-x²)
Sauf erreur...
Merci beaucoup! Après ça je fais la technique que je vous ai dite précédemment?
"j'ai posé U=U0cos(wt+) = U0ejwt et d'après l'énoncé e(t)=Ecos(wt) = Eejwt. J'ai tout remplacé, à la fin ça me fait une expression de U0 assez énorme. Est-ce correct?
Après je fais le module de U0 et son argument puis je les intègre dans l'expression : U(t)=U0cos(wt+) pour avoir U(t)
"
Enfaite c'est bon j'ai fini la question 3. J'en suis désormais à la 4.
On est actuellement entrain de commencer le cours sur l'acuité de la résonance, on a parlé vaguement de bande passante.. mais on ne l'a pas fini! Pouvez vous m'expliquer comment faire la question 4, comment on détermine la largeur?
Bonjour,
Avant de discuter de la bande passante pourriez vous donner le module de Z/(Z+r), voir sanantonio.
Ensuite, quels sont vos résultats concernant la question 3 ?
A vous lire. jed.
Bonjour tous les deux. 
Excellente question ..... dont la réponse permettra de répondre à la question 4. 
alors pour le module de Z/Z+R j'ai trouvé (je prends l'expression en fonction de Q,x et E):
|U0| = E [ Q²x²/1+x²(-2+x²+Q²) ]² + [(Qx-Qx3)/1+x²(-2+x²+Q²)]²
[ Q²x²/1+x²(-2+x²+Q²) ]² + [(Qx-Qx3)/1+x²(-2+x²+Q²)]²
La racine prend toute l'expression à partir de Q
L'amplitude de U(t) vaut E quand elle est maximale.
Si on remplace x par 1 dans toute l'expression de U(t), on a la fin : U(t) = Ecos( rt)
rt)
 U(t) = e(t) car d'après l'énoncé e(t) = Ecos(
U(t) = e(t) car d'après l'énoncé e(t) = Ecos( t)
t)
Et cela veut dire que U(t) et e(t) sont en phase non?
Si u(t) et e(t) sont en phase alors le déphasage 
 = 0?
= 0?
Bonjour,
L'amplitude maximale de u(t) est bien égale à E.
Ceci pour une pulsation wr = w0.
Alors u(t) et e(t) sont en phase (déphasage nul).
Question 4 : bande passante.
Sur la courbe U = f(w) vous recherchez les pulsations w1 et w2 telles que U = E /0,707?
.
La BP est égale à w2 - w1.
A vous lire. JED.
Sur la courbe U = f(w) vous recherchez les pulsations w1 et w2 telles que U = E /0,707.
Que voulez-vous dire par là?
Comment sait on que U = E/0.707? Je ne vois pas comment procéder, y a t-il des étapes?
Merci 
N'est-ce pas plutôt U = 0.707 E?
C'est la définition de la bande passante à -3dB. (20log( 2/2)
2/2) 20log(0.707)
20log(0.707) -3)
-3)
Au maximum, à w0, U/E=1 donc 20log(U/E)=0 dB
On cherche les 2 valeurs de w (1 de chaque côté de w0) telles que 20 log(U/E)=-3 dB.
Le calcul montre que ça consiste à cherche les valeurs de w telles que U/E= 2/2
2/2 0.707.
0.707.
C'est une définition. Donc un choix un peu arbitraire.
Tu as calculé U/E. Y'a plus qu'à y'aller. 
Et donc à la fin j'aurais une valeur w1 et une valeur w2 puis j'aurais juste à faire w2 - w1 et ça me donnera la valeur de la bande passante?
La dimension de la bande passante c'est quoi? Hz?
une différence entre 2 fréquences, ça donne une fréquence.
Mais ici, les w sont des pulsations. Donc des Rd/s. A diviser par 2 pour obtenir de Hz
pour obtenir de Hz
Bonsoir,
Vous avez U = A(x,Q)* E modules
Pour x= 1 A=1 et U = E
Pour la bande passante vous écrirez U = 0,707 E , merci sanantonio.
A(x,Q) = 0,707.................> x1, x2.............> w1, w2..........> f1,f2
Bon courage. JED.


