Niveau maths sup

Différence de marche originale

Posté par
RClausius 02-11-18 à 16:08

Bonjour à tous !

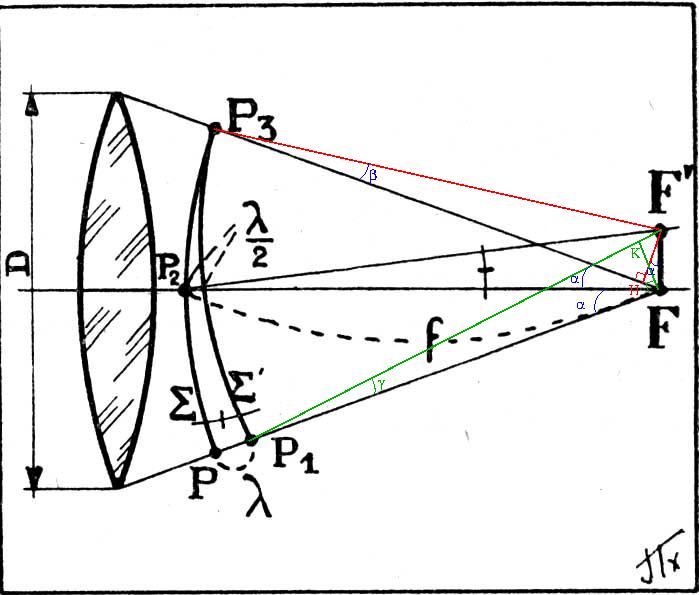
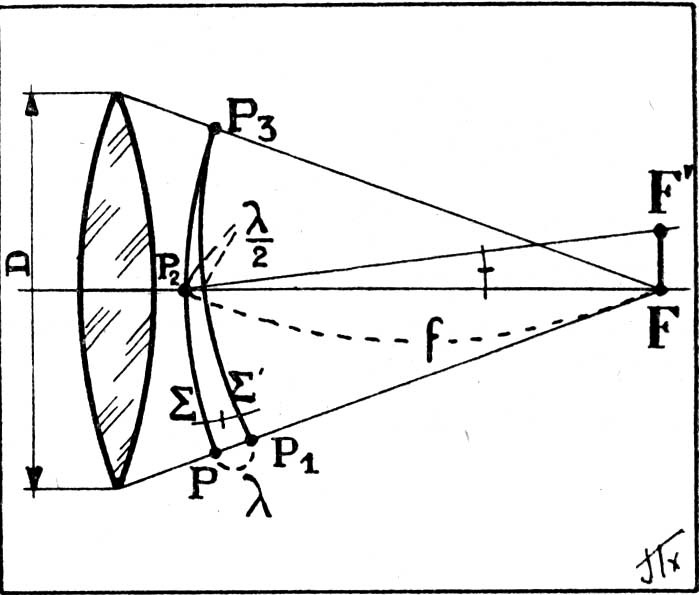
En parcourant un ouvrage sur la téléscopie, j'ai essayé sans succès de redémontrer un résultat géométrique présenté comme évident (voire la figure).
F est évidemment le foyer image de la lentille (convergente) sur laquelle arrive des rayons à l'infini (donc une onde de surface plane). La surface d'onde émergente est concentrique et de centre F ; elle est notée $\Sigma$
On suppose que le point F' est à une distance de F telle que la surface d'onde virtuelle $\Sigma '$ concentrique de centre F' et de rayon F'P_3 (le texte dit "la surface d'onde virtuelle tangente à $\Sigma$ en P_3", mais cela me semble peu rigoureux) coupe FP en P_1 (avec PP_1= $\lambda$ ).
Je suis un peu perdu, car je voudrais rester en géométrie euclidienne. Merci d'avance pour toute aide ! Et désolé du manque de clarté.

Posté par re : Différence de marche originale 02-11-18 à 18:30

Bonjour
Je crois que tu as oublié de joindre un scan du schéma...

Posté par re : Différence de marche originale 02-11-18 à 19:48

En effet, merci !

Différence de marche originale

Posté par re : Différence de marche originale 03-11-18 à 12:34

Bonjour
Il faut je pense considérer que la lentille fonctionne dans les conditions de Gauss. Dans ces conditions, sur la figure, les dimensions verticales sont très fortement "dilatées" par rapport aux dimensions horizontales et les angles entre l'axe optique et les rayons sont suffisamment petit pour que, on premier ordre près, on puisse considérer la tangente très peu différente du sinus et le cosinus très peu différent de 1.
Je note R le rayon de ' ; R=F'P₃ ;
P₃H=R.cos()R
f-R=HF=FF'.sin()
Soit K le point de la droite (P₁F') tel que FK P₁F' ;
raisonnement analogue : puisque cos()1 :
P₁FP₁K
P₁F=R-FF'.sin()
Au final :
PP₁==f-P₁F=f-R+FF'.sin()=2.FF'.sin()
Puisque :

$\sin\left(\alpha\right)=\frac{D}{2f}$

$FF'=\frac{f.\lambda}{D}$
Il y a peut-être plus simple...

Différence de marche originale