Inscription / Connexion Nouveau Sujet
Différence de marche (optique)
Bonjour,
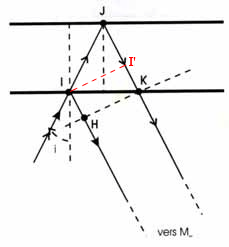
En considérant la figure ci-jointe, je cherche à déterminer la différence de marche entre les deux rayons interférant à l'infini (ceux parallèles partant vers le bas). Apparemment, ce serait . Personnellement, je crois que cette différence de marche est égale à la longueur entre le point J et le point formé par l'intersection de la droite (JK) avec le projeté orthogonal de I sur (JK); non? Si c'est bien cela, j'aurais aimé savoir pourquoi, ou du moins comment on parvient à l'expression donnée en premier lieu.
Merci d'avance!
Bonjour,
Ce n'est pas précisé...
Est-ce le même milieu partout ?
Apparemment, c'est le cas puisque les rayons vont en ligne droite mais...
Ce seraient donc des miroirs semi-réfléchissants, par exemple...
Je ne comprends pas la question.. quel "milieu"? S'il s'agit du point J, son projeté sur (IK) est bien le milieu de [IK].
On ne s'est pas compris sur le "milieu"... Je parlais du "milieu optique" puisqu'il s'agit de différence de marche "optique"... Autrement dit, si c'est du verre, de l'air ou autre...
Quoi qu'il en soit je considère que la réponse est oui.
On appelle I' le projeté orthogonal de I sur JK.
Donc
La différence de marche :
IJ + JI'- 0 = IJ + JK - KI'= IJ + JK - IH puisque IH = KI'
Désolé concernant le milieu!  En effet dans ce cas là, on supposera que l'indice est le même partout.
En effet dans ce cas là, on supposera que l'indice est le même partout.
Concernant la différence de marche, je ne saisis toujours pas le raisonnement à adopter. En effet, pourquoi est-ce égal à IJ + JI'- 0?  Quelle est la méthode suivie?
Quelle est la méthode suivie?
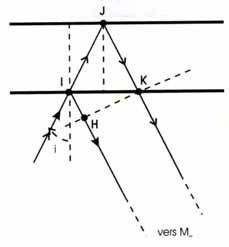
Dans la 1ère façon de voir :
Le 1er rayon parcourt IH
Le 2ème rayon parcourt IJ + JK
La différence de marche est IJ + JK - IH
Dans la 2ème façon de voir :
Le 1er rayon parcourt une distance nulle puisque l'on part du point I.
Le 2ème rayon parcourt IJ + JI'
La différence de marche est IJ + JI' - 0 = IJ + JI'
"pourquoi est-ce égal à IJ + JI'- 0 ?"==> Si cette formulation te gêne, tu peux directement dire que la différence de marche est IJ + JI', si ça te va mieux...
Ok, je te suis concernant la 1ère méthode. En revanche, la seconde me laisse perplexe.. En quoi le fait de partir du point I entraîne-t-il une distance parcourue nulle pour le premier rayon?
Merci! 
Dans la 1ère façon :
le 1er rayon parcourt IH
Le 2ème rayon parcourt IJ + JK
Dans la 2ème façon :
le 1er rayon ne parcourt rien
le 2ème rayon a la distance IH en moins à parcourir ( puisque KI' = IH )
On considère la différence de marche dans le plan II'.
Dans ce plan, à partir du point I, le 2ème rayon parcourt IJ + JI' et le 1er rayon partant du point I n'a aucune distance à parcourir puisqu'il est déjà dans ce plan lorsqu'il est réfléchi.
Il faut considérer le point I sur le rayon incident et le point I sur le rayon réfléchi. C'est le même point évidemment mais cela montre que le 1er rayon réfléchi n'a aucune distance à parcourir pour atteindre le plan II'.
C'est presque une évidence donc c'est difficile à expliquer...
Bonsoir!
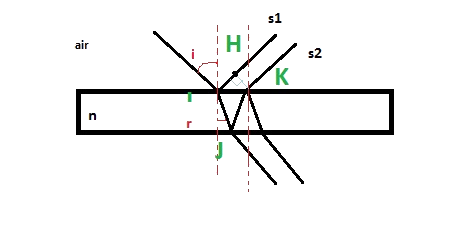
En fait, je n'ai pas dû tout saisir... J'ai essayé d'appliquer la chose à un cas tout à fait similaire (voir figure).
Selon moi, on a .
De plus, on a ,
et
, en notant
l'épaisseur de la lame.
Du coup, on aurait .
Et apparemment, ce n'est pas le cas, puisqu'on est censé trouver . Comment apparaît l'indice du milieu? Je ne vois pas l'erreur dans mon raisonnement...

C'est un problème de chemin optique...
Dans l'air, on confond le chemin géométrique et le chemin optique parce que l'indice est égal à 1.
Mais le chemin optique est en fait le chemin géométrique multiplié par l'indice.
Donc, pour le parcours dans le verre, IJ + JK doit être multiplié par n.
Disons plutôt que je l'avais oubliée... Après simplification, je retombe sur l'expression désirée, à savoir
Après simplification, je retombe sur l'expression désirée, à savoir .
Je me permets de poser un autre cas (voir image jointe, les lames sont d'égales épaisseurs). Selon mon cours, on aurait ici . Pourquoi ici l'indice n n'intervient pas? On a pourtant un trajet optique dans le milieu d'indice n?
J'aurai une autre question quand ce problème sera résolu..
Merci! 
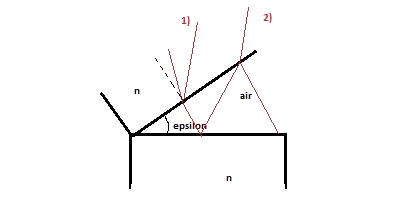
C'est un "coin" d'air formé par deux lames de verre d'égale épaisseur si j'ai bien compris...
D'ailleurs, l'épaisseur de la deuxième lame n'intervient pas a priori.
La position du rayon incident par rapport aux rayons réfléchi et réfracté me paraît bizarre  .
.
En effet, je me suis trompé concernant le rayon incident, il se place "à droite" de la normale plutôt. Ma question concernant la différence de marche reste valable, comment l'obtient-on? Je n'y parviens pas ici..
Je voudrais bien qu'on me prouve que les rayons 1 et 2 sont parallèles. Ce n'est pas évident du tout et je pense même que c'est faux...
==> Je ne vois pas pourquoi l'angle
 n'intervient pas. Que n n'intervienne pas, cela peut se comprendre, la différence de trajet étant dans l'air.
n'intervient pas. Que n n'intervienne pas, cela peut se comprendre, la différence de trajet étant dans l'air.
On peut montrer que l'angle d'incidence pour la 2ème réfraction est r+2 .
.
Sur la 1ère réflexion, on a l'angle de réflexion égal à l'angle d'incidence et n sin i = sin r.
Pour le rayon 2, on a (sauf erreur de ma part) : sin(r+2 ) = n sin i2 , i2 étant l'angle de réfraction du rayon 2.
) = n sin i2 , i2 étant l'angle de réfraction du rayon 2.
Et je ne vois pas pourquoi on aurait i2 = i .
On a :
sin i = sin r / n
et :
sin i2 = sin(r+2 ) / n
) / n
Effectivement, je pense que l'expression de la différence de marche est fausse.. Mais dans ce cas à quoi est-elle égale? Je suppose qu'on doit raisonner de la même façon que pour le premier exemple, mais avec l'angle, j'ai plus de difficultés.. Comment faire?
Si les rayons ne sont pas parallèles, je ne vois pas l'intérêt de calculer la différence de marche...
On ne peut pas appliquer le même principe que précédemment puisque les rayons n'étant pas parallèles, on ne peut plus faire de projection sur l'autre rayon.
Dans le premier cas, après le plan KH, les rayons ne subissent plus de déphasage puisqu'ils sont parallèles. Donc on peut calculer le déphasage (la différence de marche) avant KH.
correspond au cas de deux lames de verre écartées de e et parallèles.
Donc c'est peut-être le schéma qui n'est pas bon...