Inscription / Connexion Nouveau Sujet
diagramme de phase
Bonjour tout le monde,
Alors voila j'essaie de faire un exercice mais je bute à la deuxième question du II) 2.a). Pour moi l'équilibre correspondant se fait au point H( hétéroazéotrope) donc je pose ln(pa*/760)=ln(pb*/760) et je recherche T sauf que voilà je trouve T=316,83K et non 357,3K. Je suis vraiment perdu SVP est ce que quelqu'un pourrait m'aider.
Voici l'énoncé:
On veut déterminer précisément le diagramme isobare P=760mmHg eau-toluène.On dispose pour cela des valeurs des pression de vapeurs saturantes de l'eau(A) et du toluène (B) fournies par les relations suivantes:
ln(pa*/760)=13,899-5176,4/T et ln(pb*/760)=11,962-4562,7/T
II.2) Monter que lorsque l'au et le toluène coexiste dans les phases liquides et gaz la température est de 357,3K
1)Ecrire l'équilibre correspondant.Où obtient-on cette coexistence.
2)Quelle relation vérifient pa* et pb*? En déduire à la température de 357,3K les valeurs pa* et pb*.
Bonjour
J'appelle x la fraction molaire en eau, la fraction molaire en toluène étant (1-x) tant que le mélange est homogène (au dessus de la courbe de rosée).
Je choisis d'utiliser l'atmosphère comme unité de pression ; cela évite de traîner des 780 partout. La pression totale est P°=1atm.
Au dessus de la courbe de rosée les pressions partielles sont :
PA=x.P° ; PB=(1-x).P°
Courbe de rosée pour x<xH :
Sur la courbe de rosée, il y a équilibre entre le mélange des deux vapeurs et la première goutte de toluène formé. La pression partielle PB est donc égale à la pression de vapeur saturante de B : P*B.
Les deux logarithmes des pressions sont égaux, cela donne :
D'où l'équation de la courbe de rosée pour x>xH :
Courbe de rosée pour x>xH :
Sur la courbe, la vapeur est en équilibre avec la première goutte d'eau formée ; la pression partielle en vapeur d'eau dans le mélange est égale à la pression de valeur saturante de l'eau. Cela conduit à :
D'où l'équation de la courbe de rosée pour x>xH :
En écrivant que les deux courbes se coupent en H, tu peux calculer les valeurs de xH et TH ;
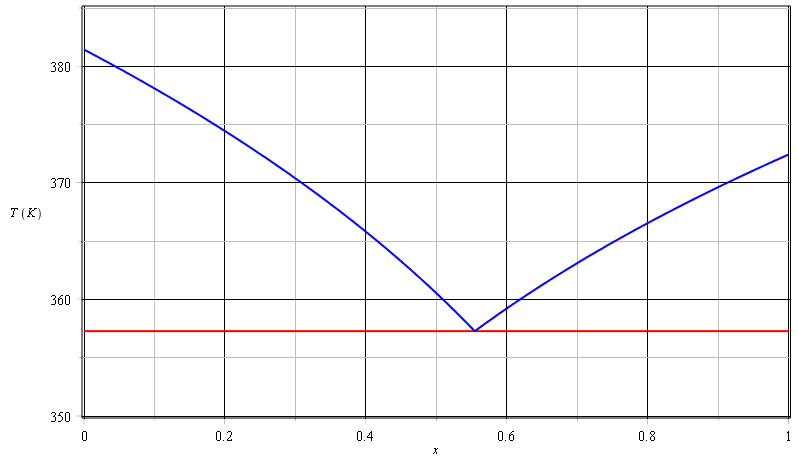
Je te laisse faire les calculs. Voici tout de même les courbes :